已知函数f(x)=x3-3x及y=f(x)上一点P(1,-2),过点P作直线l.
(1)求使直线l和y=f(x)相切且以P为切点的直线方程;
(2)求使直线l和y=f(x)相切且切点异于P的直线方程y=g(x);
(3)在(2)的条件下,求F(x)=f(x)+tg(x)(t为常数)在[2,+∞)上单调时,t的取值范围.
解:(1)由f(x)=x
3-3x得,f′(x)=3x
2-3,
过点P且以P(1,-2)为切点的直线的斜率f′(1)=0,
∴所求直线方程为y=-2.
(2)设过P(1,-2)的直线l与y=f(x)切于另一点(x
0,y
0),
则f′(x
0)=3x
02-3.
又直线过(x
0,y
0),P(1,-2),
故其斜率可表示为
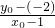
=
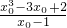
,
又
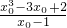
=3x
02-3,
即x
03-3x
0+2=3(x
02-1)•(x
0-1),
解得x
0=1(舍)或x
0=-

,
故所求直线的斜率为k=3×(

-1)=-

,
∴y-(-2)=-

(x-1),
即9x+4y-1=0.
(3)由(2)得g(x)=-

x+

,则F(x)=x
3-3x+t(-

x+

),
∴F′(x)=3x
3-(

t+3),
当

t+3≤0时,F(x)≥0在[2,+∞)上恒成立,F(x)在[2,+∞)上是增函数;
当

t+3>0时,由F′(x)=0得极值点:x
1=-
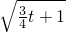
,x
2=
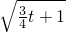
,
在
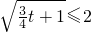
,即
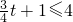
,即t≤4时,F(x)在[2,+∞)上是增函数,
∴t的取值范围:t≤4.
分析:(1)由已知可得斜率函数为f′(x)=3x
2-3,进而求出所过点切线的斜率,代入点斜式公式即可.
(2)设另一切点为(x
0,y
0),求出该点切线方程,再由条件列方程计算.
(3)由(2)得g(x)=-

x+

,则F(x)=x
3-3x+t(-

x+

),求其导数,再分类讨论:当

t+3≤0时,F(x)≥0在[2,+∞)上恒成立,F(x)在[2,+∞)上是增函数;当

t+3>0时,求得当t≤4时,F(x)在[2,+∞)上是增函数,从而求出t的取值范围.
点评:本小题主要考查利用导数研究曲线上某点切线方程′、利用导数研究函数的单调性等基础知识,考查运算求解能力,考查化归与转化思想.属于基础题.

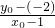 =
=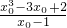 ,
,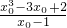 =3x02-3,
=3x02-3, ,
, -1)=-
-1)=- ,
, (x-1),
(x-1), x+
x+ ,则F(x)=x3-3x+t(-
,则F(x)=x3-3x+t(- x+
x+ ),
), t+3),
t+3), t+3≤0时,F(x)≥0在[2,+∞)上恒成立,F(x)在[2,+∞)上是增函数;
t+3≤0时,F(x)≥0在[2,+∞)上恒成立,F(x)在[2,+∞)上是增函数; t+3>0时,由F′(x)=0得极值点:x1=-
t+3>0时,由F′(x)=0得极值点:x1=-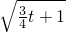 ,x2=
,x2=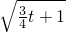 ,
,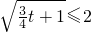 ,即
,即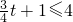 ,即t≤4时,F(x)在[2,+∞)上是增函数,
,即t≤4时,F(x)在[2,+∞)上是增函数, x+
x+ ,则F(x)=x3-3x+t(-
,则F(x)=x3-3x+t(- x+
x+ ),求其导数,再分类讨论:当
),求其导数,再分类讨论:当 t+3≤0时,F(x)≥0在[2,+∞)上恒成立,F(x)在[2,+∞)上是增函数;当
t+3≤0时,F(x)≥0在[2,+∞)上恒成立,F(x)在[2,+∞)上是增函数;当 t+3>0时,求得当t≤4时,F(x)在[2,+∞)上是增函数,从而求出t的取值范围.
t+3>0时,求得当t≤4时,F(x)在[2,+∞)上是增函数,从而求出t的取值范围.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<