练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知双曲线-=1(b∈N*)的左、右两个焦点为F1、F2,P是双曲线上的一点,且满足|PF1||PF2|=|F1F2|2,|PF2|<4.

    (1)求b的值;

    (2)抛物线y2=2px(p>0)的焦点与该双曲线的右顶点重合,斜率为1的直线经过右顶点,与该抛物线交于A、B两点,求弦长|AB|.

     

    【答案】

    (1) b=1 (2)16

    【解析】

    解:(1)根据题意a2=4,a=2,又a2+b2=c2,

    ||PF1|-|PF2||=2a=4,

    |PF1|·|PF2|=|F1F2|2=4c2,|PF2|<4,

    得|PF2|2+4|PF2|-4c2=0在区间(0,4)上有解,

    所以c2<8,因此b2<4,

    又b∈N*,所以b=1.

    (2)双曲线方程为-y2=1,右顶点坐标为(2,0),

    所以抛物线方程为y2=8x,①

    直线方程为y=x-2,②

    由①②两式联立,解得

    和

    所以弦长|AB|==16.

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知双曲线=1(a＞0,b＞0)的动弦BC平行于虚轴，M、N是双曲线的左、右顶点,

    (1)求直线MB、CN的交点P的轨迹方程；

    (2)若P(x1,y1)，B(x2,y2),求证:a是x1、x2的比例中项.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知双曲线=1(a＞b＞0)的左、右焦点分别为F1(-c,0)、F2(c,0)(c＞0),P是双曲线右支上的一点,在上的投影的绝对值恰好为||,且它们的夹角为,则双曲线的离心率为

    A.               B.+1                C.                 D.2

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年山西省晋中市昔阳中学高二（上）第二次月考数学试卷（理科）（解析版） 题型：解答题

    已知双曲线=1（a＞0，b＞0）的离心率为，右准线方程为．
    （Ⅰ）求双曲线C的方程；
    （Ⅱ）已知直线x-y+m=0与双曲线C交于不同的两点A，B，且线段AB的中点在圆x2+y2=5上，求m的值．

    查看答案和解析>>

    科目：高中数学 来源：《第2章 圆锥曲线与方程》2012年单元测试卷（南宁外国语学校）（解析版） 题型：解答题

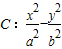    已知双曲线=1（a＞0，b＞0）的离心率为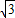，右准线方程为．
    （Ⅰ）求双曲线C的方程；
    （Ⅱ）已知直线x-y+m=0与双曲线C交于不同的两点A，B，且线段AB的中点在圆x2+y2=5上，求m的值．

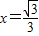    查看答案和解析>>

    同步练习册答案