
【题目】一个工厂在某年连续10个月每月产品的总成本y(万元)与该月产量x(万件)之间有如下一组数据:
x | 1.08 | 1.12 | 1.19 | 1.28 | 1.36 | 1.48 | 1.59 | 1.68 | 1.80 | 1.87 |
y | 2.25 | 2.37 | 2.40 | 2.55 | 2.64 | 2.75 | 2.92 | 3.03 | 3.14 | 3.26 |
(1)通过画散点图,发现可用线性回归模型拟合y与x的关系,请用相关系数加以说明;
(2)①建立月总成本y与月产量x之间的回归方程;
②通过建立的y关于x的回归方程,估计某月产量为1.98万件时,此时产品的总成本为多少万元?
(均精确到0.001)
附注:①参考数据:![]() ,
,
![]() ,
,
②参考公式:相关系数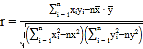 ,
,
回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: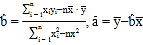 .
.
 精英口算卡系列答案
精英口算卡系列答案科目:高中数学 来源: 题型:
【题目】用0,1,2,3,4,5这六个数字组成无重复数字的四位数.
(1)在组成的四位数中,求所有偶数的个数;
(2)在组成的四位数中,求比2430大的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆C:![]() (a>b>0)的左、右焦点分别为
(a>b>0)的左、右焦点分别为![]() ,离心率为
,离心率为![]() ,过焦点
,过焦点![]() 且垂直于x轴的直线被椭圆C截得的线段长为1.
且垂直于x轴的直线被椭圆C截得的线段长为1.
(Ⅰ)求椭圆C的方程;
(Ⅱ)已知点M(0,-1),直线l经过点N(2,1)且与椭圆C相交于A,B两点(异于点M),记直线MA的斜率为![]() ,直线MB的斜率为
,直线MB的斜率为![]() ,证明
,证明![]() 为定值,并求出该定值.
为定值,并求出该定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 过点
过点![]() ,其参数方程为
,其参数方程为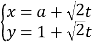 (
(![]() 为参数,
为参数, ![]() ),以
),以![]() 为极点,
为极点, ![]() 轴非负半轴为极轴,建立极坐标系,曲线
轴非负半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)求已知曲线![]() 和曲线
和曲线![]() 交于
交于![]() 两点,且
两点,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}为正项等比数列,a1+a2=6,a3=8.
(1)求数列{an}的通项公式an;
(2)若bn=![]() ,且{bn}前n项和为Tn,求Tn.
,且{bn}前n项和为Tn,求Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex+1-alnax+a(a>0).
(1)当a=1时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)若关于x的不等式f(x)>0恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4—4:坐标系与参数方程]
在直角坐标系![]() 中,曲线
中,曲线![]() 的方程为
的方程为![]() .以坐标原点为极点,
.以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() 与
与![]() 有且仅有三个公共点,求
有且仅有三个公共点,求![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,矩形![]() 中,
中,![]() ,
,![]() 是
是![]() 边上异于端点的动点,
边上异于端点的动点,![]() ,将矩形
,将矩形![]() 沿
沿![]() 折叠至
折叠至![]() 处,使面
处,使面![]() (如图2).点
(如图2).点![]() 满足
满足![]() ,
,![]() .
.
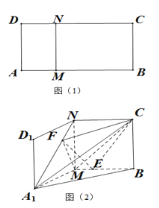
(1)证明:![]() ;
;
(2)设![]() ,当
,当![]() 为何值时,四面体
为何值时,四面体![]() 的体积最大,并求出最大值.
的体积最大,并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 、
、![]() 分别为双曲线
分别为双曲线![]() 的左右焦点,左右顶点为
的左右焦点,左右顶点为![]() 、
、![]() ,
,![]() 是双曲线上任意一点,则分别以线段
是双曲线上任意一点,则分别以线段![]() 、
、![]() 为直径的两圆的位置关系为( )
为直径的两圆的位置关系为( )
A. 相交B. 相切C. 相离D. 以上情况均有可能
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com