
分析 设数列{an}的前n项和为Sn.由题意可得:$\frac{n}{{a}_{1}+{a}_{2}+…+{a}_{n}}$=$\frac{1}{2n-1}$,即Sn=2n2-n,利用递推关系即可得出.
解答 解:设数列{an}的前n项和为Sn.
由题意可得:$\frac{n}{{a}_{1}+{a}_{2}+…+{a}_{n}}$=$\frac{1}{2n-1}$,
∴Sn=2n2-n,
∴n=1时,a1=S1=1;
n≥2时,an=Sn-Sn-1=2n2-n-[2(n-1)2-(n-1)]=4n-3,
n=1时上式也成立,
∴an=4n-3.
故答案为:4n-3.
点评 本题考查了新定义“倒均数”、数列递推关系、数列通项公式,考查了推理能力与计算能力,属于中档题.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
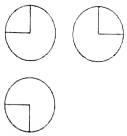 如图,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径,半径长度为2,则该几何体的表面积是( )
如图,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径,半径长度为2,则该几何体的表面积是( )| A. | 17π | B. | 18π | C. | 20π | D. | 28π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 分层抽样 | B. | 抽签法 | C. | 随机数表法 | D. | 系统抽样法 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -4 | B. | -2 | C. | -1 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com