
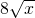 千吨.
千吨.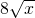 千吨,可得
千吨,可得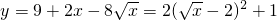 .
. ,即x=4(小时)时,蓄水池的水量最少,只有1千吨.
,即x=4(小时)时,蓄水池的水量最少,只有1千吨. 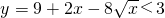 .
.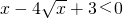
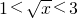
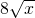 千吨,可得函数解析式,利用配方法,可得结论;
千吨,可得函数解析式,利用配方法,可得结论;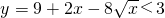 ,解不等式,即可求得结论.
,解不等式,即可求得结论.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:单选题
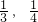 ,假定他们两人的行动相互不受影响,则暑假期间游客甲、游客乙两人都不去西安看世园会的概率为
,假定他们两人的行动相互不受影响,则暑假期间游客甲、游客乙两人都不去西安看世园会的概率为



查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com