

分析 (1)根据已知中抛物线与坐标轴的交点,构造方程组,解得抛物线的解析式;
(2)设y=x+b(b<-3)与抛物线切于E点,则此时△EBC的面积最大,联立方程求出E点坐标,可得答案;
(3)先求出P点坐标,再根据旋转变换公式,可得满足条件的M点的坐标.
解答 解:(1)∵抛物线y=ax2+bx+c与x轴交于A(-1,0),B(3,0),与y轴交与点C(0,-3).
∴$\left\{\begin{array}{l}a-b+c=0\\ 9a+3b+c=0\\ c=-3\end{array}\right.$,
解得$\left\{\begin{array}{l}a=1\\ b=-2\\ c=-3\end{array}\right.$,
∴抛物线的解析式为y=x2-2x-3;
(2)由B(3,0),C(0,-3),
可得直线BC的方程为$\frac{x}{3}-\frac{y}{3}=1$,即y=x-3,
设y=x+b(b<-3)与抛物线切于E点,则此时△EBC的面积最大,
由$\left\{\begin{array}{l}y={x}^{2}-2x-3\\ y=x+b\end{array}\right.$得:x2-2x-(b+3)=0,
令△=0,则b=-4,
此时:x=1,y=-4,
即E点的坐标为:(1,-4);
E到BC的距离d=$\sqrt{2}$,
△EBC的面积S=$\frac{1}{2}$BC•d=3;
(3)过点C作CP∥AB交抛物线与点P,则P点坐标为(2,-3),
设M1点坐标为:(n,0),
若n=2,则PM1=3,此时对应的M点为(-1,-3)或(5,-3)点均不在抛物线上;
若n>2,则此时对应的M点为(-1,n-5),
此时n-5=1+2-3=0,解得:n=5;
故M点的坐标为(-1,0);
若n<2,则此时对应的M点为(5,5-n),
此时5-n=25-10-3=0,解得:n=-7,
故M点的坐标为(5,12),
综上M点的坐标为(-1,0)或(5,12)
点评 本题考查的知识点是二次函数的图象和性质,熟练掌握二次函数的图象和性质,是解答的关键.


科目:高中数学 来源: 题型:解答题
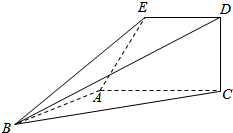 如图,已知直角梯形ACDE所在的平面垂直于平面ABC,∠BAC=90°,∠EAC=60°,AB=AC.
如图,已知直角梯形ACDE所在的平面垂直于平面ABC,∠BAC=90°,∠EAC=60°,AB=AC.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
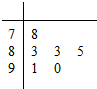 对某同学的6次物理测试成绩(满分100分)进行统计,作出的茎叶图如图所示,给出关于该同学物理成绩的以下说法:
对某同学的6次物理测试成绩(满分100分)进行统计,作出的茎叶图如图所示,给出关于该同学物理成绩的以下说法:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | l的倾斜角为锐角且不过第一象限 | B. | l的倾斜角为钝角且不过第一象限 | ||
| C. | l的倾斜角为锐角且不过第四象限 | D. | l的倾斜角为钝角且不过第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [6,+∞) | B. | [-∞,2] | C. | [-3,6] | D. | [5,6] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [2,+∞) | B. | (2,+∞) | C. | [$\frac{5}{2}$,+∞) | D. | (1,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com