
【题目】某校有1400名考生参加市模拟考试,现采取分层抽样的方法从
文、理考生中分别抽取20份和50份数学试卷,进行成绩分析,
得到下面的成绩频数分布表:
分数分组 | [0,30) | [30,60) | [60,90) | [90,120) | [120,150] |
文科频数 | 2 | 4 | 8 | 3 | 3 |
理科频数 | 3 | 7 | 12 | 20 | 8 |
(1)估计文科数学平均分及理科考生的及格人数(90分为及格分数线);
(2)在试卷分析中,发现概念性失分非常严重,统计结果如下:
文理 失分 | 文 | 理 |
概念 | 15 | 30 |
其它 | 5 | 20 |
问是否有90%的把握认为概念失分与文、理考生的不同有关?(本题可以参考独立性检验临界值表:)
| <>0.5 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式:  ,其中
,其中![]() .
.
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2x![]() ,g(x)=(4﹣lnx)lnx+b(b∈R).
,g(x)=(4﹣lnx)lnx+b(b∈R).
(1)若f(x)>0,求实数x的取值范围;
(2)若存在x1,x2∈[1,+∞),使得f(x1)=g(x2),求实数b的取值范围;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场经营的某种包装的大米质量ξ(单位:kg)服从正态分布N(10,σ2),根据检测结果可知P(9.9≤ζ≤10.1)=0.96,某公司为每位职工购买一袋这种包装的大米作为福利,若该公司有1000名职工,则分发到的大米质量在9.9kg以下的职工数大约为
A. 10 B. 20 C. 30 D. 40
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),以坐标原点为极点,以
),以坐标原点为极点,以![]() 轴的非负半轴为极轴,建立极坐标系,曲线
轴的非负半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,已知直线
,已知直线![]() 与曲线
与曲线![]() 交于不同的两点
交于不同的两点![]() ,
,![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥![]() 的底面ABCD是菱形,
的底面ABCD是菱形,![]() 平面ABCD,
平面ABCD,![]() ,
,![]() ,F,G分别为PD,BC中点,
,F,G分别为PD,BC中点,![]() .
.

(Ⅰ)求证:![]() 平面PAB;
平面PAB;
(Ⅱ)求三棱锥![]() 的体积;
的体积;
(Ⅲ)求证:OP与AB不垂直.
查看答案和解析>>
科目:高中数学 来源: 题型:
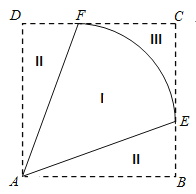
【题目】某地拟规划种植一批芍药,为了美观,将种植区域(区域I)设计成半径为1km的扇形![]() ,中心角
,中心角![]() (
(![]() ).为方便观赏,增加收入,在种植区域外围规划观赏区(区域II)和休闲区(区域III),并将外围区域按如图所示的方案扩建成正方形
).为方便观赏,增加收入,在种植区域外围规划观赏区(区域II)和休闲区(区域III),并将外围区域按如图所示的方案扩建成正方形![]() ,其中点
,其中点![]() ,
,![]() 分别在边
分别在边![]() 和
和![]() 上.已知种植区、观赏区和休闲区每平方千米的年收入分别是10万元、20万元、20万元.
上.已知种植区、观赏区和休闲区每平方千米的年收入分别是10万元、20万元、20万元.
(1)要使观赏区的年收入不低于5万元,求![]() 的最大值;
的最大值;
(2)试问:当![]() 为多少时,年总收入最大?
为多少时,年总收入最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com