
【题目】如图,四边形![]() 是平行四边形,平面
是平行四边形,平面![]()
![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.
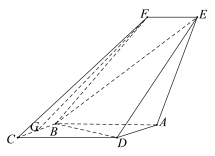
(1)求证:![]()
![]() 平面
平面![]() ;
;
(2)求证:![]()
![]() 平面
平面![]() ;
;
(3)求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(1)见证明;(2)见证明;(3)![]()
【解析】
(1)取![]() 的中点
的中点![]() ,通过证明四边形
,通过证明四边形![]() 是平行四边形,可得到
是平行四边形,可得到![]()
![]()
![]() ,从而得证;
,从而得证;
(2)由余弦定理证得![]() ,通过平面
,通过平面![]() 平面
平面![]() 即可得证;
即可得证;
(3)由![]()
![]() 平面
平面![]() ,所以点
,所以点![]() 到平面
到平面![]() 的距离等于点
的距离等于点![]() 到平面
到平面![]() 的距离,通过
的距离,通过![]() 计算距离即可.
计算距离即可.
(1)证明:取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]()
在![]() 中,因为
中,因为![]() 是
是![]() 的中点,
的中点,
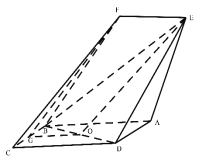
所以![]()
![]()
![]() 且
且![]() ,
,
因为![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]() ,
,
所以![]()
![]()
![]() 且
且![]() ,
,
所以四边形![]() 是平行四边形,所以
是平行四边形,所以![]()
![]()
![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]()
![]() 平面
平面![]() .
.
(2)证明:在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
由余弦定理得![]() ,
,
因为![]() ,
,
所以![]() .
.
因为平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(3)解法1:由(1)![]()
![]() 平面
平面![]() ,
,
所以点![]() 到平面
到平面![]() 的距离等于点
的距离等于点![]() 到平面
到平面![]() 的距离,
的距离,
设点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,
,
过![]() 作
作![]() ,交
,交![]() 的延长线于
的延长线于![]() ,
,
则![]() 平面
平面![]() ,所以
,所以![]() 是三棱锥
是三棱锥![]() 的高
的高
由余弦定理可得![]() ,
,
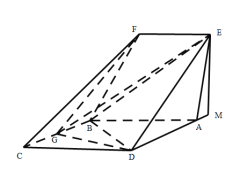
所以![]() ,
,![]() .
.
![]()
![]() .
.
因为![]() ,
,
即![]() ,解得
,解得![]() .
.
所以点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.
解法2:因为![]()
![]()
![]() ,且
,且![]() ,
,
所以点![]() 到平面
到平面![]() 的距离等于点
的距离等于点![]() 到平面
到平面![]() 的距离的
的距离的![]() ,
,
由(2)![]() 面
面![]() .
.
因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
过点![]() 作
作![]() 于点
于点![]() ,又因为平面
,又因为平面![]() 平面
平面![]() ,故
,故![]() 平面
平面![]() .
.

所以![]() 为点
为点![]() 到平面
到平面![]() 的距离.
的距离.
在![]() 中,
中,![]() ,
,
由余弦定理可得![]()
所以![]() ,
,
因此![]() ,
,
所以点![]() 到平面
到平面![]() 的距离为
的距离为![]()


 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:高中数学 来源: 题型:
【题目】ΔABC的内角A,B,C的对边分别为a,b,c,根据下列条件解三角形,其中有两解的是
A. a=2,b=3,A=30°B. b=6,c=4,A=120°
C. a=4![]() ,b=6,A=60°D. a=3,b=6,A=30°
,b=6,A=60°D. a=3,b=6,A=30°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了适应高考改革,某中学推行“创新课堂”教学.高一平行甲班采用“传统教学”的教学方式授课,高一平行乙班采用“创新课堂”的教学方式授课,为了比较教学效果,期中考试后,分别从两个班中各随机抽取![]() 名学生的成绩进行统计分析,结果如下表:(记成绩不低于
名学生的成绩进行统计分析,结果如下表:(记成绩不低于![]() 分者为“成绩优秀”)
分者为“成绩优秀”)
分数 |
|
|
|
|
|
|
|
甲班频数 |
|
|
|
|
|
|
|
乙班频数 |
|
|
|
|
|
|
|
(1)由以上统计数据填写下面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 以上的把握认为“成绩优秀与教学方式有关”?
以上的把握认为“成绩优秀与教学方式有关”?
甲班 | 乙班 | 总计 | |
成绩优秀 | |||
成绩不优秀 | |||
总计 |
(2)在上述样本中,学校从成绩为![]() 的学生中随机抽取
的学生中随机抽取![]() 人进行学习交流,求这
人进行学习交流,求这![]() 人来自同一个班级的概率.
人来自同一个班级的概率.
参考公式:![]() ,其中
,其中![]() .
.
临界值表
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2015年1月至2017年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是()
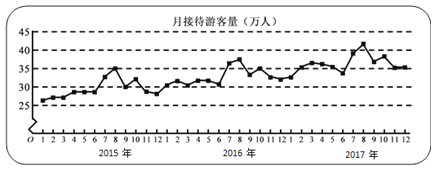
A. 年接待游客量逐年增加
B. 各年的月接待游客量高峰期在8月
C. 2015年1月至12月月接待游客量的中位数为30万人
D. 各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】临川一中实验学校坐落在抚州火车站附近,在校区东边(如图),有一直径为8米的半圆形空地,现计划移植一古树,但需要有辅助光照.半圆周上的![]() 处恰有一可旋转光源满足古树生长的需要,该光源照射范围是
处恰有一可旋转光源满足古树生长的需要,该光源照射范围是![]() ,点
,点![]() 在直径
在直径![]() 上,且
上,且![]() .
.
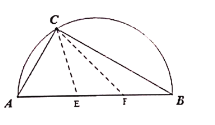
(1)若![]() ,求
,求![]() 的长;
的长;
(2)设![]() ,求该空地种植古树的最大面积.
,求该空地种植古树的最大面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了变废为宝,节约资源,新上了一个从生活垃圾中提炼生物柴油的项目.经测算该项目月处理成本![]() (元)与月处理量
(元)与月处理量![]() (吨)之间的函数关系可以近似地表示为:
(吨)之间的函数关系可以近似地表示为: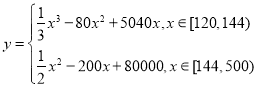 ,且每处理一吨生活垃圾,可得到能利用的生物柴油价值为
,且每处理一吨生活垃圾,可得到能利用的生物柴油价值为![]() 元,若该项目不获利,政府将给予补贴.
元,若该项目不获利,政府将给予补贴.
(1)当![]() 时,判断该项目能否获利?如果获利,求出最大利润;如果不获利,则政府每月至少需要补贴多少元才能使该项目不亏损?
时,判断该项目能否获利?如果获利,求出最大利润;如果不获利,则政府每月至少需要补贴多少元才能使该项目不亏损?
(2)该项目每月处理量为多少吨时,才能使每吨的平均处理成本最低?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱ABC﹣A1B1C1中,侧面ABB1A1为菱形且∠BAA1=60°,D,M分别为CC1和A1B的中点,A1D⊥CC1,AA1=A1D=2,BC=1.
(1)证明:直线MD∥平面ABC;
(2)求D点到平面ABC的距离.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com