
【题目】已知椭圆 ![]() 的中心在原点,焦点在
的中心在原点,焦点在 ![]() 轴上,长轴长为4,且点
轴上,长轴长为4,且点 ![]() 在椭圆
在椭圆 ![]() 上.
上.
(1)求椭圆 ![]() 的方程;
的方程;
(2)设 ![]() 是椭圆
是椭圆 ![]() 长轴上的一个动点,过
长轴上的一个动点,过 ![]() 作斜率为
作斜率为 ![]() 的直线
的直线 ![]() 交椭圆
交椭圆 ![]() 于
于 ![]() 、
、 ![]() 两点,求证:
两点,求证: ![]() 为定值.
为定值.
【答案】
(1)解:因为 ![]() 的焦点在
的焦点在 ![]() 轴上且长轴长为4,
轴上且长轴长为4,
故可设椭圆 ![]() 的方程为
的方程为 ![]()
因为点 ![]() 在椭圆
在椭圆 ![]() 上,所以
上,所以 ![]()
解得 ![]() .
.
所以,椭圆 ![]() 的方程为
的方程为 ![]()
(2)证明:设 ![]() ,由已知,直线
,由已知,直线 ![]() 的方程是
的方程是 ![]() ,
,
由  消去
消去 ![]() 得,
得, ![]()
设 ![]() ,则
,则 ![]() 是方程
是方程 ![]() 的两个根,
的两个根,
所以有, ![]() ,因为 |PA|2+|PB|2=(x1-m)2+y12+(x2-m)2+y22
,因为 |PA|2+|PB|2=(x1-m)2+y12+(x2-m)2+y22
所以, ![]() 为定值
为定值
【解析】(1)根据椭圆的性质可知a=4,c2=a2-b2 , 再将 ( 1 ,![]() ) 代入椭圆求解即可。
) 代入椭圆求解即可。
(2)设出直线l的方程,联立椭圆,根据韦达定理可以得到x1和x2的关系,再代入 |PA|2+|PB|2中即可得证。
【考点精析】本题主要考查了椭圆的标准方程的相关知识点,需要掌握椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() 才能正确解答此题.
才能正确解答此题.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:高中数学 来源: 题型:
【题目】已知一元二次方程x2+(1+a)x+a+b+1=0的两个实根为x1,x2,且0<x1<1,x2>1,则 ![]() 的取值范围是( )
的取值范围是( )
A.(-2,- ![]() )
)
B.(-1,- ![]() )
)
C.(-2, ![]() )
)
D.(-1, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,a,b,c分别是∠A,∠B,∠C的对边,已知a=![]() c.
c.
(1)若∠A=2∠B,求cosB;
(2)若AC=2,求△ABC面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】每年的4月23日为世界读书日,为调查某高校学生(学生很多)的读书情况,随机抽取了男生,女生各20人组成的一个样本,对他们的年阅读量(单位:本)进行了统计,分析得到了男生年阅读量的频率分布表和女生阅读量的频率分布直方图. 男生年阅读量的频率分布表(年阅读量均在区间[0,60]内):
本/年 | [0,10) | [10,20) | [20,30) | [30,40) | [40,50) | [50,60] |
频数 | 3 | 1 | 8 | 4 | 2 | 2 |
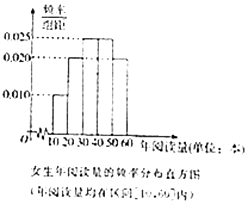
(1)根据女生的频率分布直方图估计该校女生年阅读量的中位数;
(2)在样本中,利用分层抽样的方法,从男生年与度量在[20,30),[30,40)的两组里抽取6人,再从这6人中随机抽取2人,求[30,40)这一组中至少有1人被抽中的概率;
(3)若年阅读量不小于40本为阅读丰富,否则为阅读不丰富,依据上述样本研究阅读丰富与性别的关系,完成下列2×2列联表,并判断是否有99%的把握认为月底丰富与性别有关.
性别 阅读量 | 丰富 | 不丰富 | 合计 |
男 | |||
女 | |||
合计 |
P(K2≥k0) | 0.025 | 0.010 | 0.005 |
k0 | 5.024 | 6.635 | 7.879 |
附:K2= ![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
查看答案和解析>>
科目:高中数学 来源: 题型:
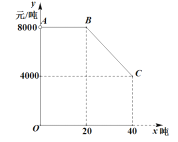
【题目】乔经理到老陈的果园里一次性采购一种水果,他俩商定:乔经理的采购价![]() (元/吨)与采购量
(元/吨)与采购量![]() (吨)之间函数关系的图像如图中的折线段
(吨)之间函数关系的图像如图中的折线段![]() 所示(不包含端点
所示(不包含端点![]() 但包含端点
但包含端点![]() ).
).
(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)已知老陈种植水果的成本是2800元/吨,那么乔经理的采购量为多少时,老陈在这次买卖中所获的利润![]() 最大?最大利润是多少?
最大?最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确的是( )
A.如果平面 ![]() 平面
平面 ![]() ,则
,则 ![]() 内任意一条直线必垂直于
内任意一条直线必垂直于 ![]()
B.若直线 ![]() 不平行于平面
不平行于平面 ![]() ,则
,则 ![]() 内不存在直线平行于直线
内不存在直线平行于直线 ![]()
C.如果平面 ![]() 不垂直于平面
不垂直于平面 ![]() ,那么平面
,那么平面 ![]() 内一定不存在直线垂直于平面
内一定不存在直线垂直于平面 ![]()
D.若直线 ![]() 不垂直于平面
不垂直于平面 ![]() ,则
,则 ![]() 内不存在直线垂直于直线
内不存在直线垂直于直线 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市电视台为了提高收视率而举办有奖问答活动,随机对该市15~65岁的人群抽样了 ![]() 人,回答问题统计结果及频率分布直方图如图表所示.
人,回答问题统计结果及频率分布直方图如图表所示.
(1)分别求出 ![]() 的值;
的值;
(2)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,则第2,3,4组每组应各抽取多少人?
(3)在(2)的前提下,电视台决定在所抽取的6人中随机抽取2人颁发幸运奖,求所抽取的人中第2组至少有1人获得幸运奖的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com