
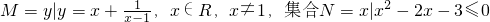 ,则
,则 (x≠1)的值域,即可求出集合M,解x2-2x-3≤0,可得集合N;据此分析选项,可得答案.
(x≠1)的值域,即可求出集合M,解x2-2x-3≤0,可得集合N;据此分析选项,可得答案. =(x-1)+
=(x-1)+ +1,(x≠1)
+1,(x≠1)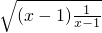 +1=3,
+1=3, =-[(1-x)+
=-[(1-x)+ ]+1≤-1,
]+1≤-1, (x≠1)的值域为{x|x≤-1或x≥3},
(x≠1)的值域为{x|x≤-1或x≥3}, (x≠1)的值域,则M={x|x≤-1或x≥3},
(x≠1)的值域,则M={x|x≤-1或x≥3}, (x≠1)的值域,求出集合M,求其值域时,注意不要遗漏x<1的情况.
(x≠1)的值域,求出集合M,求其值域时,注意不要遗漏x<1的情况. 

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com