
ΓΨΧβΡΩΓΩΡ≥≥§ –ΦΤΜ°œζ έΡ≥÷÷ ≥ΤΖΘ§œ÷―ϊ«κΦΉΓΔ““ΝΫΗω…ΧΦ“Ϋχ≥Γ ‘œζ10ΧλΘ°ΝΫΗω…ΧΦ“ΧαΙ©ΒΡΖΒάϊΖΫΑΗ»γœ¬ΘΚΦΉ…ΧΦ“ΟΩΧλΙΧΕ®ΖΒάϊ60‘ΣΘ§«“ΟΩ¬τ≥ω“ΜΦΰ ≥ΤΖ…ΧΦ“‘ΌΖΒάϊ3‘ΣΘΜ““…ΧΦ“ΈόΙΧΕ®ΖΒάϊΘ§¬τ≥ω30Φΰ“‘ΡΎΘ®Κ§30ΦΰΘ©ΒΡ ≥ΤΖΘ§ΟΩΦΰ ≥ΤΖ…ΧΦ“ΖΒάϊ5‘ΣΘ§≥§≥ω30ΦΰΒΡ≤ΩΖ÷ΟΩΦΰΖΒάϊ8‘ΣΘ°Ψ≠Ά≥ΦΤΘ§ΝΫΗω…ΧΦ“ΒΡ ‘œζ«ιΩωΨΞ“ΕΆΦ»γœ¬ΘΚ
Θ®1Θ©œ÷¥”ΦΉ…ΧΦ“ ‘œζΒΡ10Χλ÷–≥ι»ΓΝΫΧλΘ§«σ’βΝΫΧλΒΡœζ έΝΩΕΦ–Γ”Ύ30ΒΡΗ≈¬ ΘΜ
Θ®2Θ©»τΫΪΤΒ¬ ”ΉςΗ≈¬ Θ§ΜΊ¥π“‘œ¬Έ ΧβΘΚ
ΔΌ Φ«…ΧΦ“““ΒΡ»’ΖΒάϊΕνΈΣXΘ®ΒΞΈΜΘΚ‘ΣΘ©Θ§«σXΒΡΖ÷≤ΦΝ–ΚΆ ΐ―ßΤΎΆϊΘΜ
ΔΎ ≥§ –Ρβ‘ΎΦΉΓΔ““ΝΫΗω…ΧΦ“÷–―Γ‘ώ“ΜΦ“≥ΛΤΎœζ έΘ§»γΙϊΫω¥”»’ΤΫΨυΖΒάϊΕνΒΡΫ«Ε»ΩΦ¬«Θ§«κάϊ”ΟΥυ―ßΒΡΆ≥ΦΤ―ß÷Σ ΕΈΣ≥§ –Ής≥ω―Γ‘ώΘ§≤ΔΥΒΟςάμ”…Θ°
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() ΘΜΘ®2Θ©ΔΌΦϊΫβΈωΘΜΔΎΦϊΫβΈω.
ΘΜΘ®2Θ©ΔΌΦϊΫβΈωΘΜΔΎΦϊΫβΈω.
ΓΨΫβΈωΓΩ ‘ΧβΖ÷ΈωΘΚΘ®1Θ©ΫαΚœΉιΚœ÷Σ ΕΘ§άϊ”ΟΙ≈ΒδΗ≈–ΆΗ≈¬ ΙΪ ΫΦ¥Ω…«σΝΫΧλΒΡœζ έΝΩΕΦ–Γ”Ύ![]() ΒΡΗ≈¬ ΘΜΘ®2Θ©ΔΌ
ΒΡΗ≈¬ ΘΜΘ®2Θ©ΔΌ![]() ΒΡΥυ”–Ω…Ρή»Γ÷ΒΈΣΘΚ
ΒΡΥυ”–Ω…Ρή»Γ÷ΒΈΣΘΚ ![]() Θ§
Θ§ ![]() Θ§
Θ§ ![]() Θ§
Θ§ ![]() Θ§
Θ§ ![]() Θ§ΗυΨίΙ≈ΒδΗ≈–ΆΗ≈¬ ΙΪ ΫΘ§«σ≥ωΗςΗωΥφΜζ±δΝΩΕ‘”ΠΒΡΗ≈¬ Θ§¥”ΕχΩ…ΒΟ
Θ§ΗυΨίΙ≈ΒδΗ≈–ΆΗ≈¬ ΙΪ ΫΘ§«σ≥ωΗςΗωΥφΜζ±δΝΩΕ‘”ΠΒΡΗ≈¬ Θ§¥”ΕχΩ…ΒΟ![]() ΒΡΖ÷≤ΦΝ–Θ§ΫχΕχΩ…ΒΟΤΎΆϊ÷ΒΘΜΔΎœ»«σ≥ωΦΉ…ΧΦ“ΒΡ»’ΤΫΨυœζ έΝΩΘ§¥”ΕχΩ…ΒΟΦΉ…ΧΦ“ΒΡ»’ΤΫΨυΖΒάϊΕνΘ§‘Ό”…ΔΌΒΟ≥ω““…ΧΦ“ΒΡ»’ΤΫΨυΖΒάϊΕνΘ§±»ΫœΖΒάϊΕνΒΡ¥σ–ΓΩ…ΒΟΫα¬έ.
ΒΡΖ÷≤ΦΝ–Θ§ΫχΕχΩ…ΒΟΤΎΆϊ÷ΒΘΜΔΎœ»«σ≥ωΦΉ…ΧΦ“ΒΡ»’ΤΫΨυœζ έΝΩΘ§¥”ΕχΩ…ΒΟΦΉ…ΧΦ“ΒΡ»’ΤΫΨυΖΒάϊΕνΘ§‘Ό”…ΔΌΒΟ≥ω““…ΧΦ“ΒΡ»’ΤΫΨυΖΒάϊΕνΘ§±»ΫœΖΒάϊΕνΒΡ¥σ–ΓΩ…ΒΟΫα¬έ.
‘ΧβΫβΈωΘΚΘ®1Θ©Φ«ΓΑ≥ι»ΓΒΡΝΫΧλœζ έΝΩΕΦ–Γ”Ύ30Γ±ΈΣ ¬ΦΰAΘ§
‘ρP(A)= ![]() =
=![]() Θ°
Θ°
Θ®2Θ©…η““…ΧΦ“ΒΡ»’œζ έΝΩΈΣaΘ§‘ρ
Β±a=28 ±Θ§X=28ΓΝ5=140ΘΜ
Β±a=29 ±Θ§X=29ΓΝ5=145ΘΜ
Β±a=30 ±Θ§X=30ΓΝ5=150ΘΜ
Β±a=31 ±Θ§X=30ΓΝ5+1ΓΝ8=158ΘΜ
Β±a=32 ±Θ§X=30ΓΝ5+2ΓΝ8=166ΘΜ
Υυ“‘XΒΡΥυ”–Ω…Ρή»Γ÷ΒΈΣΘΚ140Θ§145Θ§150Θ§158Θ§166Θ°
Υυ“‘XΒΡΖ÷≤ΦΝ–ΈΣ
X | 140 | 145 | 150 | 158 | 166 |
P |
|
|
|
|
|
Υυ“‘EX=140ΓΝ![]() +145ΓΝ
+145ΓΝ![]() +150ΓΝ
+150ΓΝ![]() +158ΓΝ
+158ΓΝ![]() +166ΓΝ
+166ΓΝ![]() =152.8.
=152.8.
ΔΎ“άΧβ“βΘ§ΦΉ…ΧΦ“ΒΡ»’ΤΫΨυœζ έΝΩΈΣΘΚ28ΓΝ0.2+29ΓΝ0.4+30ΓΝ0.2+31ΓΝ0.1+32ΓΝ0.1=29.5
Υυ“‘ΦΉ…ΧΦ“ΒΡ»’ΤΫΨυΖΒάϊΕνΈΣΘΚ60+29.5ΓΝ3=148.5‘ΣΘ°
”…ΔΌΒΟ““…ΧΦ“ΒΡ»’ΤΫΨυΖΒάϊΕνΈΣ152.8‘ΣΘ®ΘΨ148.5‘ΣΘ©Θ§
Υυ“‘ΆΤΦωΗΟ≥§ –―Γ‘ώ““…ΧΦ“≥ΛΤΎœζ έΘ°


 –ΡΥψΩΎΥψ«…Υψ“ΜΩΈ“ΜΝΖœΒΝ–¥πΑΗ
–ΡΥψΩΎΥψ«…Υψ“ΜΩΈ“ΜΝΖœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΈΣΝΥΖ¥”≥ΙζΟώΨ≠ΦΟΗς––“ΒΕ‘≤÷¥ΔΈοΝς“ΒΈώΒΡ–η«σ±δΜ·«ιΩωΘ§“‘ΦΑ÷Ί“Σ…ΧΤΖΩβ¥φ±δΜ·ΒΡΕ·œρΘ§÷–ΙζΈοΝς”κ≤…ΙΚΝΣΚœΜαΚΆ÷–¥ΔΖΔ’ΙΙ…Ζί”–œόΙΪΥΨΆ®ΙΐΝΣΚœΒς≤ιΘ§÷ΤΕ®ΝΥ÷–Ιζ≤÷¥Δ÷Η ΐΘ°»γΆΦΥυ ΨΒΡ’έœΏΆΦ «2016Ρξ1‘¬÷Ν2017Ρξ12‘¬ΒΡ÷–Ιζ≤÷¥Δ÷Η ΐΉΏ Τ«ιΩωΘ°
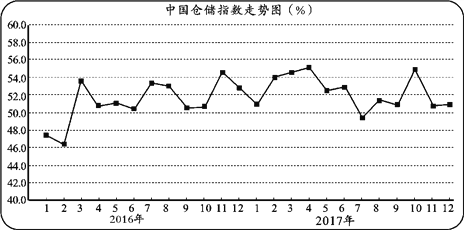
ΗυΨίΗΟ’έœΏΆΦΘ§œ¬Ν–Ϋα¬έ’ΐ»ΖΒΡ «
A. 2016ΡξΗς‘¬ΒΡ≤÷¥Δ÷Η ΐΉν¥σ÷Β «‘Ύ3‘¬Ζί
B. 2017Ρξ1‘¬÷Ν12‘¬ΒΡ≤÷¥Δ÷Η ΐΒΡ÷–ΈΜ ΐΈΣ54%
C. 2017Ρξ1‘¬÷Ν4‘¬ΒΡ≤÷¥Δ÷Η ΐ±»2016ΡξΆ§ΤΎ≤®Ε·–‘Ηϋ¥σ
D. 2017Ρξ11‘¬ΒΡ≤÷¥Δ÷Η ΐΫœ…œ‘¬”–ΥυΜΊ¬δΘ§œ‘ Ψ≥ω≤÷¥Δ“ΒΈώΜνΕ·»‘»ΜΫœΈΣΜν‘ΨΘ§Ψ≠ΦΟ‘Υ––Έ»÷–œρΚΟ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σy=fΘ®xΘ© «Ε®“ε‘ΎΘ®Θ≠ΓόΘ§+ΓόΘ©…œΒΡΤφΚ· ΐΘ§«“‘ΎΘέ0Θ§+ΓόΘ©…œΈΣ‘ωΚ· ΐΘ§
Θ®1Θ©«σ÷ΛΘΚΚ· ΐ‘ΎΘ®Θ≠ΓόΘ§0Θ©…œ“≤ «‘ωΚ· ΐΘΜ
Θ®2Θ©»γΙϊfΘ®![]() Θ©=1Θ§Ϋβ≤ΜΒ» ΫΘ≠1ΘΦfΘ®2x+1Θ©Γή0Θ°
Θ©=1Θ§Ϋβ≤ΜΒ» ΫΘ≠1ΘΦfΘ®2x+1Θ©Γή0Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΓΨ―Γ–ό4-4ΘΚΉχ±ξœΒ”κ≤Έ ΐΖΫ≥ΧΓΩ
‘Ύ÷±Ϋ«Ήχ±ξœΒ![]() ÷–Θ§«ζœΏ
÷–Θ§«ζœΏ![]() ΒΡ≤Έ ΐΖΫ≥ΧΈΣ
ΒΡ≤Έ ΐΖΫ≥ΧΈΣ![]() Θ®
Θ®![]() ΈΣ≤Έ ΐΘ©Θ§“‘Ήχ±ξ‘≠Βψ
ΈΣ≤Έ ΐΘ©Θ§“‘Ήχ±ξ‘≠Βψ![]() ΈΣΦΪΒψΘ§
ΈΣΦΪΒψΘ§![]() ÷αΒΡ’ΐΑκ÷αΈΣΦΪ÷αΫ®ΝΔΦΪΉχ±ξœΒΘ§«ζœΏ
÷αΒΡ’ΐΑκ÷αΈΣΦΪ÷αΫ®ΝΔΦΪΉχ±ξœΒΘ§«ζœΏ![]() ΒΡΦΪΉχ±ξΖΫ≥ΧΈΣ
ΒΡΦΪΉχ±ξΖΫ≥ΧΈΣ![]() .
.
Θ®ΔώΘ©«σ«ζœΏ![]() ΒΡΦΪΉχ±ξΖΫ≥ΧΚΆ
ΒΡΦΪΉχ±ξΖΫ≥ΧΚΆ![]() ΒΡ÷±Ϋ«Ήχ±ξΖΫ≥ΧΘΜ
ΒΡ÷±Ϋ«Ήχ±ξΖΫ≥ΧΘΜ
Θ®ΔρΘ©÷±œΏ![]() ”κ«ζœΏ
”κ«ζœΏ![]() Ζ÷±πΫΜ”ΎΒΎ“ΜœσœόΡΎΒΡ
Ζ÷±πΫΜ”ΎΒΎ“ΜœσœόΡΎΒΡ![]() Θ§
Θ§![]() ΝΫΒψΘ§«σ
ΝΫΒψΘ§«σ![]() .
.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩœ¬±μ «20ΗωΙζΦ“ΚΆΒΊ«χΒΡΕΰ―θΜ·ΧΦ≈≈Ζ≈ΉήΝΩΦΑ»ΥΨυΕΰ―θΜ·ΧΦ≈≈Ζ≈ΝΩ.
ΙζΦ“ΚΆΒΊ«χ | ≈≈Ζ≈ΉήΝΩ/«ßΕ÷ | »ΥΨυ≈≈Ζ≈ΝΩ/Ε÷ | ΙζΦ“ΚΆΒΊ«χ | ≈≈Ζ≈ΉήΝΩ/«ßΕ÷ | »ΥΨυ≈≈Ζ≈ΝΩ/Ε÷ | |
A | 10330000 | 7.4 | K | 480000 | 2.0 | |
B | 5300000 | 16.6 | L | 480000 | 7.5 | |
C | 3740000 | 7.3 | M | 470000 | 3.9 | |
D | 2070000 | 1.7 | N | 410000 | 5.3 | |
E | 1800000 | 12.6 | O | 390000 | 16.9 | |
F | 1360000 | 10.7 | P | 390000 | 6.4 | |
G | 840000 | 10.2 | Q | 370000 | 5.7 | |
H | 630000 | 12.7 | R | 330000 | 6.2 | |
I | 550000 | 15.7 | S | 320000 | 6.2 | |
J | 510000 | 2.6 | T | 490000 | 16.6 |
Θ®1Θ©’β20ΗωΙζΦ“ΚΆΒΊ«χ»ΥΨυΕΰ―θΜ·ΧΦ≈≈Ζ≈ΝΩΒΡ÷–ΈΜ ΐ «Εύ…ΌΘΩ
Θ®2Θ©’κΕ‘’β20ΗωΙζΦ“ΚΆΒΊ«χΘ§«κΡψ’“≥ωΕΰ―θΜ·ΧΦ≈≈Ζ≈ΉήΝΩΫœ…ΌΒΡ«Α15%ΒΡΙζΦ“ΚΆΒΊ«χ.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»τACΓΆBCΘ§AC=BC=1Θ§ΒψP «ΓςABCΡΎ“ΜΒψΘ§‘ρ![]() ΒΡ»Γ÷ΒΖΕΈß «Θ®ΓΓΓΓΘ©
ΒΡ»Γ÷ΒΖΕΈß «Θ®ΓΓΓΓΘ©
A. Θ®©¹![]() Θ§0Θ© B. Θ®0Θ§
Θ§0Θ© B. Θ®0Θ§![]() Θ© C. Θ®©¹
Θ© C. Θ®©¹![]() Θ§
Θ§![]() Θ© D. Θ®©¹1Θ§1Θ©
Θ© D. Θ®©¹1Θ§1Θ©
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐ![]() Θ®Τδ÷–
Θ®Τδ÷–![]() Θ©Θ°
Θ©Θ°
Θ®1Θ©Β±![]() ±Θ§«σ
±Θ§«σ![]() ΝψΒψΒΡΗω ΐkΒΡ÷ΒΘΜ
ΝψΒψΒΡΗω ΐkΒΡ÷ΒΘΜ
Θ®2Θ©‘ΎΘ®1Θ©ΒΡΧθΦΰœ¬Θ§Φ«’β–©ΝψΒψΖ÷±πΈΣ![]() Θ§«σ÷ΛΘΚ
Θ§«σ÷ΛΘΚ ![]() Θ°
Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΓΑ―νΜ‘»ΐΫ«Γ± «Έ“Ιζ ΐ―ß Ζ…œΒΡ“ΜΗωΈΑ¥σ≥…ΨΆΘ§ «Εΰœν ΫœΒ ΐ‘Ύ»ΐΫ«–Έ÷–ΒΡ“Μ÷÷ΦΗΚΈ≈≈Ν–.»γΆΦΥυ ΨΘ§»Ξ≥ΐΥυ”–ΈΣ1ΒΡœνΘ§“ά¥ΥΙΙ≥… ΐΝ–2Θ§3Θ§3Θ§4Θ§6Θ§4Θ§5Θ§10Θ§10Θ§5Θ§Γ≠Θ§‘ρ¥Υ ΐΝ–ΒΡ«Α56œνΚΆΈΣ_____.

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΈΣΝΥΫβ»ΥΟ«Ε‘ΓΑ―”≥ΌΆΥ–ίΡξΝδ’ΰ≤ΏΓ±ΒΡΧ§Ε»Θ§Ρ≥≤ΩΟ≈¥”ΡξΝδ‘Ύ![]() ΥξΒΫ
ΥξΒΫ![]() ΥξΒΡ»Υ»Κ÷–ΥφΜζΒς≤ιΝΥ
ΥξΒΡ»Υ»Κ÷–ΥφΜζΒς≤ιΝΥ![]() »ΥΘ§≤ΔΒΟΒΫ»γΆΦΥυ ΨΒΡΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΘ§‘Ύ’β
»ΥΘ§≤ΔΒΟΒΫ»γΆΦΥυ ΨΒΡΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΘ§‘Ύ’β![]() »Υ÷–≤Μ÷ß≥÷ΓΑ―”≥ΌΆΥ–ίΡξΝδ’ΰ≤ΏΓ±ΒΡ»Υ ΐ”κΡξΝδΒΡΆ≥ΦΤΫαΙϊ»γΆΦΥυ ΨΘΚ
»Υ÷–≤Μ÷ß≥÷ΓΑ―”≥ΌΆΥ–ίΡξΝδ’ΰ≤ΏΓ±ΒΡ»Υ ΐ”κΡξΝδΒΡΆ≥ΦΤΫαΙϊ»γΆΦΥυ ΨΘΚ

ΡξΝδ | ≤Μ÷ß≥÷ΓΑ―”≥ΌΆΥ–ίΡξΝδ’ΰ≤ΏΓ±ΒΡ»Υ ΐ |
|
|
|
|
|
|
|
|
|
|
Θ®1Θ©”…ΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΘ§ΙάΦΤ’β![]() »ΥΡξΝδΒΡΤΫΨυ ΐΘΜ
»ΥΡξΝδΒΡΤΫΨυ ΐΘΜ
Θ®2Θ©ΗυΨί“‘…œΆ≥ΦΤ ΐΨίΧν–¥œ¬ΟφΒΡ![]() Ν–ΝΣ±μΘ§Ψί¥Υ±μΘ§ΡήΖώ‘ΎΖΗ¥μΈσΒΡΗ≈¬ ≤Μ≥§Ιΐ
Ν–ΝΣ±μΘ§Ψί¥Υ±μΘ§ΡήΖώ‘ΎΖΗ¥μΈσΒΡΗ≈¬ ≤Μ≥§Ιΐ![]() ΒΡ«ΑΧαœ¬Θ§»œΈΣ“‘
ΒΡ«ΑΧαœ¬Θ§»œΈΣ“‘![]() ΥξΈΣΖ÷ΫγΒψΒΡ≤ΜΆ§»Υ»ΚΕ‘ΓΑ―”≥ΌΆΥ–ίΡξΝδ’ΰ≤ΏΓ±ΒΡΧ§Ε»¥φ‘Ύ≤ν“λΘΩ
ΥξΈΣΖ÷ΫγΒψΒΡ≤ΜΆ§»Υ»ΚΕ‘ΓΑ―”≥ΌΆΥ–ίΡξΝδ’ΰ≤ΏΓ±ΒΡΧ§Ε»¥φ‘Ύ≤ν“λΘΩ
45Υξ“‘œ¬ | 45Υξ“‘…œ | ΉήΦΤ | |
≤Μ÷ß≥÷ | |||
÷ß≥÷ | |||
ΉήΦΤ |
ΗΫΘΚ![]()
≤ΈΩΦ ΐΨίΘΚ
|
|
|
|
|
|
|
|
|
|
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com