
【题目】如图为某校语言类专业N名毕业生的综合测评成绩(百分制)分布直方图,已知80~90分数段的学员数为21人. (Ⅰ)求该专业毕业总人数N和90~95分数段内的人数n;
(Ⅱ)现欲将90~95分数段内的n名人分配到几所学校,从中安排2人到甲学校去,若n人中仅有两名男生,求安排结果至少有一名男生的概率.
【答案】解:(Ⅰ)80~90分数段频率为P1=(0.04+0.03)×5=0.35, 此分数段的学员总数为21人所以毕业生,
的总人数N为N= ![]() =60,
=60,
90~95分数段内的人数频率为P1=1﹣(0.01+0.04+0.05+0.04+0.03+0.01)×5=0.1
所以90~95分数段内的人数n=60×0.1=6,
(Ⅱ) 90~95分数段内的6人中有两名男生,4名女生
设男生为1,2;女生为3,4,5,6,设安排结果中至少有一名男生为事件A
从中取两名毕业生的所有情况(基本事件空间)为12,13,14,15,16,23,24,25,26,34,35,36,45,46,56共15种组合方式,
每种组合发生的可能性是相同的,其中,至少有一名男生的种数为12,13,14,15,16,23,24,25,26共9种
所以,P(A)= ![]() =
= ![]()
【解析】(Ⅰ)根据频率分布直方图,先求出80~90分数段频率,即可求出N,再用1减去成绩落在其它区间上的频率,即得成绩落在90~95上的频率,继而期初该段的人数(Ⅱ)一一列举出所有的基本事件,再找到满足条件的基本事件,根据概率公式计算即可
【考点精析】本题主要考查了频率分布直方图的相关知识点,需要掌握频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息才能正确解答此题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】△ABC的三个顶点分别为A(0,4)、B(-2,6)、C(-8,0).
(1)分别求边AC和AB所在直线的方程;
(2)求AC边上的中线BD所在直线的方程;
(3)求AC边的中垂线所在直线的方程;
(4)求AC边上的高所在直线的方程;
(5)求经过两边AB和AC的中点的直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在正方体ABCD-A′B′C′D′中: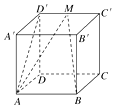
(1)求二面角D′-AB-D的大小;
(2)若M是C′D′的中点,求二面角M-AB-D的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在R上且以2为周期的偶函数,当0≤x≤1,f(x)=x2 . 如果函数g(x)=f(x)﹣(x+m)有两个零点,则实数m的值为( )
A.2k(k∈Z)
B.2k或2k+ ![]() (k∈Z)
(k∈Z)
C.0
D.2k或2k﹣ ![]() (k∈Z)
(k∈Z)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】求圆心在直线 x 2 y 3 = 0 上,且过点A(2,-3),B(-2,-5)的圆C的方程.
(1)求圆心在直线 ![]() 上,且过点A(2,-3),B(-2,-5)的圆C的方程.
上,且过点A(2,-3),B(-2,-5)的圆C的方程.
(2)设 ![]() 是圆C上的点,求
是圆C上的点,求 ![]() 的最大值和最小值.
的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() ,
, ![]() ,设函数
,设函数 ![]() .
.
(1)求函数 ![]() 的单调递增区间;
的单调递增区间;
(2)在 ![]() 中,边
中,边 ![]() 分别是角
分别是角 ![]() 的对边,角
的对边,角 ![]() 为锐角,若
为锐角,若![]() ,
, ![]() ,
, ![]() 的面积为
的面积为 ![]() ,求边
,求边 ![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,两个正方形 ![]() 和
和 ![]() 所在平面互相垂直,设
所在平面互相垂直,设 ![]() 分别是
分别是 ![]() 和
和 ![]() 的中点,那么
的中点,那么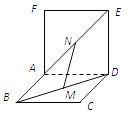
① ![]() ; ②
; ② ![]() 平面
平面 ![]() ;③
;③ ![]() ;④
;④ ![]() 异面,其中假命题的个数为( )
异面,其中假命题的个数为( )
A.4
B.3
C.2
D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且满足a1= ![]() ,2Sn﹣SnSn﹣1=1(n≥2).
,2Sn﹣SnSn﹣1=1(n≥2).
(1)求S1 , S2 , S3 , S4并猜想Sn的表达式(不必写出证明过程);
(2)设bn= ![]() ,n∈N*,求bn的最大值.
,n∈N*,求bn的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设Sn为数列{cn}的前n项和,an=2n , bn=50﹣3n,cn= ![]() .
.
(1)求c4与c8的等差中项;
(2)当n>5时,设数列{Sn}的前n项和为Tn .
(ⅰ)求Tn;
(ⅱ)当n>5时,判断数列{Tn﹣34ln}的单调性.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com