
设函数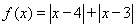 ,
,
(1)求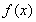 的最小值
的最小值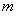 ;
;
(2)当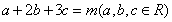 时,求
时,求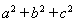 的最小值.
的最小值.
(1)1;(2)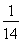
【解析】
试题分析:(1)因为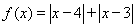 ,所以通过绝对值的基本不等式
,所以通过绝对值的基本不等式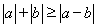 ,即可得到最小值.另外也可以通过分类关键是去绝对值,求出不同类的函数式的最小值,再根据这些最小值中的最小值确定所求的结论.
,即可得到最小值.另外也可以通过分类关键是去绝对值,求出不同类的函数式的最小值,再根据这些最小值中的最小值确定所求的结论.
(2)由(1)求出的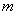 的值,所以得到
的值,所以得到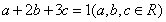 .再根据柯西不等式即可求得
.再根据柯西不等式即可求得 的最小值.同时强调等号成立的条件.
的最小值.同时强调等号成立的条件.
试题解析:(1)法1: f(x)=|x-4|+|x-3|≥|(x-4)-(x-3)|=1,
故函数f(x)的最小值为1. m=1. 法2: . x≥4时,f(x)≥1;x<3时,f(x)>1,3≤x<4时,f(x)=1,故函数f(x)的最小值为1. m=1.
. x≥4时,f(x)≥1;x<3时,f(x)>1,3≤x<4时,f(x)=1,故函数f(x)的最小值为1. m=1.
(2)由柯西不等式(a2+b2+c2)(12+22+32)≥(a+2b+3c)2=1故a2+b2+c2≥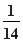
当且仅当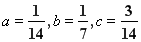 时取等号
时取等号
考点:1.绝对值不等式.2.柯西不等式.3.最值的问题.


科目:高中数学 来源:2011-2012学年江苏省扬州市宝应县高三下学期期初测试数学试卷 题型:解答题
(本题满分14分)设函数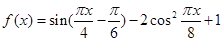 .
.
(1)求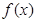 的最小正周期.
的最小正周期.
(2)若函数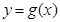 与
与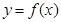 的图像关于直线
的图像关于直线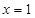 对称,求当
对称,求当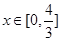 时
时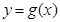 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年广西柳铁一中高三第二次月考文科数学卷 题型:解答题
已知向量 ,设函数
,设函数 。
。
(1)求 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
(2)在△ABC中,角A、B、C所对的边分别为 ,若
,若 △ABC面积为
△ABC面积为 ,求
,求 的值。
的值。
查看答案和解析>>
科目:高中数学 来源:2012届福建南安侨光中学高三第三次阶段考理科数学试卷 题型:解答题
已知向量 ,设函数
,设函数 。
。
(1)求 的最小正周期与单调递减区间。
的最小正周期与单调递减区间。
(2)在 中,
中, 、
、 、
、 分别是角
分别是角 、
、 、
、 的对边,若
的对边,若 的面积为
的面积为 ,求
,求 的值
的值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com