
分析 由$\frac{{a}_{i}}{3a-{a}_{i}}$=$\frac{3a-(3a-{a}_{i})}{3a-{a}_{i}}$=$\frac{3a}{3a-{a}_{i}}$-1,可得f(a1,a2,a3,…an)=$\sum_{i=1}^{n}$$\frac{{a}_{i}}{3a-{a}_{i}}$=($\frac{3a}{3a-{a}_{1}}$+$\frac{3a}{3a-{a}_{2}}$+…+$\frac{3a}{3a-{a}_{n}}$-n),求出[(3a-a1)+(3a-a2)+…+(3a-an)]•($\frac{3a}{3a-{a}_{1}}$+$\frac{3a}{3a-{a}_{2}}$+…+$\frac{3a}{3a-{a}_{n}}$-n)≥an,
则f(a1,a2,a3,…an)=$\sum_{i=1}^{n}$$\frac{{a}_{i}}{3a-{a}_{i}}$=($\frac{3a}{3a-{a}_{1}}$+$\frac{3a}{3a-{a}_{2}}$+…+$\frac{3a}{3a-{a}_{n}}$-n)的值可求.
解答 解:∵$\frac{{a}_{i}}{3a-{a}_{i}}$=$\frac{3a-(3a-{a}_{i})}{3a-{a}_{i}}$=$\frac{3a}{3a-{a}_{i}}$-1,
∴f(a1,a2,a3,…an)=$\sum_{i=1}^{n}$$\frac{{a}_{i}}{3a-{a}_{i}}$=($\frac{3a}{3a-{a}_{1}}$+$\frac{3a}{3a-{a}_{2}}$+…+$\frac{3a}{3a-{a}_{n}}$-n)
∴[(3a-a1)+(3a-a2)+…+(3a-an)]•($\frac{3a}{3a-{a}_{1}}$+$\frac{3a}{3a-{a}_{2}}$+…+$\frac{3a}{3a-{a}_{n}}$-n)
=3a[(3a-a1)+(3a-a2)+…+(3a-an)]•($\frac{1}{3a-{a}_{1}}$+$\frac{1}{3a-{a}_{2}}$+…+$\frac{1}{3a-{a}_{n}}$)-[(3a-a1)+(3a-a2)+…+(3a-an)]×n
=3a[(3a-a1)+(3a-a2)+…+(3a-an)]•($\frac{1}{3a-{a}_{1}}$+$\frac{1}{3a-{a}_{2}}$+…+$\frac{1}{3a-{a}_{n}}$)-a(3n-1)n
≥3a(n+2$\sqrt{\frac{3a-{a}_{1}}{3a-{a}_{2}}•\frac{3a-{a}_{2}}{3a-{a}_{1}}}$+2$\sqrt{\frac{3a-{a}_{1}}{3a-{a}_{3}}•\frac{3a-{a}_{3}}{3a-{a}_{1}}}$+…+2$\sqrt{\frac{3a-{a}_{n-1}}{3a-{a}_{n}}•\frac{3a-{a}_{n}}{3a-{a}_{n-1}}}$)-a(3n-1)n
=3a•[n+2($\frac{{n}^{2}-n}{2}$)]-3an2+an=an.
上式当且仅当a1=a2=a3=…=an时等号成立.
∴f(a1,a2,a3,…an)=$\sum_{i=1}^{n}$$\frac{{a}_{i}}{3a-{a}_{i}}$=$\frac{3a}{3a-{a}_{1}}$+$\frac{3a}{3a-{a}_{2}}$+…+$\frac{3a}{3a-{a}_{n}}$-n
≥$\frac{an}{(3a-{a}_{1})+(3a-{a}_{2})+…+(3a-{a}_{n})}$=$\frac{an}{3an-a}=\frac{n}{3n-1}$.
点评 本题是数列与函数的综合题,考查了利用基本不等式求函数的最值,关键是考查灵活变形能力,难度较大.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:选择题
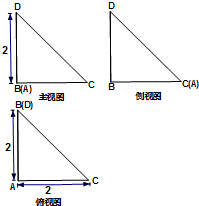 如图所示是三棱锥D-ABC的三视图,若在三棱锥的直观图中,点O为线段BC的中点,则异面直线DC与AB所成角的余弦值等于( )
如图所示是三棱锥D-ABC的三视图,若在三棱锥的直观图中,点O为线段BC的中点,则异面直线DC与AB所成角的余弦值等于( )| A. | $\frac{{\sqrt{6}}}{6}$ | B. | $\frac{{\sqrt{6}}}{3}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{5}}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ④ | D. | ①②③ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
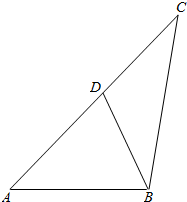 如图,在△ABC中,AB=2,AC=4,线段CB的垂直平分线交线段AC于D,AD-DB=1,则△BCD的面积为( )
如图,在△ABC中,AB=2,AC=4,线段CB的垂直平分线交线段AC于D,AD-DB=1,则△BCD的面积为( )| A. | $\frac{7}{10}$ | B. | $\frac{9}{10}$ | C. | 2 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com