如图所示，两个不全等的△ABC与△A1B1C1分别在两个互相平行的平面内，它们的边两两对应平行．求证：多面体A1B1C1－ABC为棱台．
|
证明：∵A1B1∥AB，∴A1B1与AB确定平面α．
同理，B1C1与BC确定平面β，C1A1与CA确定平面γ． 又∵△ABC与△A1B1C1不全等，∴A1B1≠AB ∴平面α内的两直线AA1与BB1必相交，不妨设交点为P． ∴P∈AA1 ∴AA1、BB1与CC1延长后相交于一点(如图所示)．∴P－ABC为三棱锥． ∵△A1B1C1是被平行于△ABC所在的平面所截， 
练习册系列答案
相关习题
科目：高中数学 来源： 题型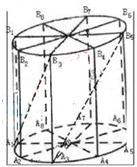：  如图所示，为了制作一个圆柱形灯笼，先要制作4个全等的矩形骨架，总计耗用9.6米铁丝，骨架把圆柱底面8等份，再用S平方米塑料片制成圆柱的侧面和下底面（不安装上底面）．（1）当圆柱底面半径r取何值时，S取得最大值？并求出该最大值（结果精确到0.01平方米）； （2）在灯笼内，以矩形骨架的顶点为点，安装一些霓虹灯，当灯笼的底面半径为0.3米时，求图中两根直线A1B3与A3B5所在异面直线所成角的大小（结果用反三角函数表示） 查看答案和解析>> 科目：高中数学 来源： 题型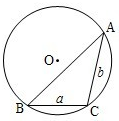：  通常用a、b、c表示△ABC的三个内角∠A、∠B、∠C所对边的边长，R表示△ABC外接圆半径．（1）如图所示，在以O为圆心，半径为2的⊙O中，BC和BA是⊙O的弦，其中BC=2，∠ABC=45°，求弦AB的长； （2）在△ABC中，若∠C是钝角，求证：a2+b2＜4R2； （3）给定三个正实数a、b、R，其中b≤a，问：a、b、R满足怎样的关系时，以a、b为边长，R为外接圆半径的△ABC不存在，存在一个或两个（全等的三角形算作同一个）？在△ABC存在的情况下，用a、b、R表示c． 查看答案和解析>> 科目：高中数学 来源： 题型： 如图所示，为了制作一个圆柱形灯笼，先要制作4个全等的矩形骨架，总计耗用9.6米铁丝，骨架把圆柱底面8等份，再用S平方米塑料片制成圆柱的侧面和下底面（不安装上底面）. (1)当圆柱底面半径 最大值（结果精确到0.01平方米）; （2）在灯笼内，以矩形骨架的顶点为点，安装一些霓虹灯，当灯笼的底面半径为0.3米时，求图中两根直线
查看答案和解析>> 同步练习册答案 湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区 违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com版权声明：本站所有文章，图片来源于网络，著作权及版权归原作者所有，转载无意侵犯版权，如有侵权，请作者速来函告知，我们将尽快处理，联系qq：3310059649。 ICP备案序号: 沪ICP备07509807号-10 鄂公网安备42018502000812号 |
γ，P∈BB1
取何值时，
取得最大值？并求出该
与
所在异面直线所成角的大小（结果用反三角函数表示）
(1)当圆柱底面半径
取何值时，
取得最大值？并求出该
与
所在异面直线所成角的大小（结果用反三角函数表示）