
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,以
中,以![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,圆
轴正半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为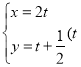 为参数),直线
为参数),直线![]() 和圆
和圆![]() 交于
交于![]() 两点,
两点,![]() 是圆
是圆![]() 上不同于
上不同于![]() 的任意一点.
的任意一点.
(1)求圆心的极坐标;
(2)求点![]() 到直线
到直线![]() 的距离的最大值.
的距离的最大值.
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln (x+1)-![]() -x,a∈R.
-x,a∈R.
(1)当a>0时,求函数f(x)的单调区间;
(2)若存在x>0,使f(x)+x+1<-![]() (a∈Z)成立,求a的最小值.
(a∈Z)成立,求a的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究小组为了研究某品牌智能手机在正常使用情况下的电池供电时间,分别从该品牌手机的甲、乙两种型号中各选取![]() 部进行测试,其结果如下:
部进行测试,其结果如下:
甲种手机供电时间(小时) |
|
|
|
|
|
|
乙种手机供电时间(小时) |
|
|
|
|
|
|
(1)求甲、乙两种手机供电时间的平均值与方差,并判断哪种手机电池质量好;
(2)为了进一步研究乙种手机的电池性能,从上述![]() 部乙种手机中随机抽取
部乙种手机中随机抽取![]() 部,记所抽
部,记所抽![]() 部手机供电时间不小于
部手机供电时间不小于![]() 小时的个数为
小时的个数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来我国电子商务行业迎来发展的新机遇,与此同时,相关管理部门推出了针对电商商品和服务的评价体系.现从评价系统中选出200次成功交易,并对其评价进行统计,对商品好评率为![]() ,对服务好评率为
,对服务好评率为![]() ,其中对商品和服务都做出好评的交易为80次.
,其中对商品和服务都做出好评的交易为80次.
(1)是否可以在犯错误率不超过0.1%的前提下,认为商品好评与服务好评有关?
(2)若针对商品的好评率,采用分层抽样的方式从这200次交易中取出5次交易,并从中选择两次交易进行客户回访,求只有一次好评的概率.
注:1.
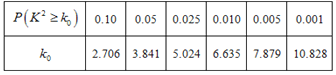
注2. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an+1﹣2an}是公比为2的等比数列,其中a1=1,a2=4.
(1)证明:数列{ ![]() }是等差数列;
}是等差数列;
(2)求数列{an}的前n项和Sn;
(3)记Cn= ![]() (n≥2),证明:
(n≥2),证明: ![]() (
( ![]() )n<
)n< ![]() +…+
+…+ ![]() ≤1﹣(
≤1﹣( ![]() )n﹣1 .
)n﹣1 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋子里有编号为![]() 的五个球,某位教师从袋中任取两个不同的球. 教师把所取两球编号的和只告诉甲,其乘积只告诉乙,让甲、乙分别推断这两个球的编号.
的五个球,某位教师从袋中任取两个不同的球. 教师把所取两球编号的和只告诉甲,其乘积只告诉乙,让甲、乙分别推断这两个球的编号.
甲说:“我无法确定.”
乙说:“我也无法确定.”
甲听完乙的回答以后,甲又说:“我可以确定了.”
根据以上信息, 你可以推断出抽取的两球中
A. 一定有3号球 B. 一定没有3号球 C. 可能有5号球 D. 可能有6号球
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com