练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知α，β∈（ ，π），sin（α+β）=﹣ ，sin（β﹣ ）= ，则cos（α+ ）=（ ）
    A.
    B.
    C.﹣
    D.﹣

    【答案】C
    【解析】解：∵α，β∈（ ，π），
    ∴α+β∈（ ，2π），β﹣ ∈（ ， ），
    ∵sin（α+β）=﹣ ，sin（β﹣ ）= ，
    ∴cos（α+β）= ，cos（β﹣ ）=﹣ ，
    则cos（α+ ）=cos[（α+β）﹣（β﹣ ）]=cos（α+β）cos（β﹣ ）+sin（α+β）sin（β﹣ ）= ×（﹣ ）+（﹣ ）× =﹣ ．
    故选C
    【考点精析】通过灵活运用两角和与差的余弦公式和两角和与差的正弦公式，掌握两角和与差的余弦公式：；两角和与差的正弦公式：即可以解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】黄种人群中各种血型的人所占的比例如下：

    血型

    A

    B

    AB

    O

    该血型的人所占比例(%)

    28

    29

    8

    35

    已知同种血型的人可以输血，O型血可以输给任何一种血型的人，其他不同血型的人不能互相输血，小明是B型血，若小明因病需要输血，问：

    (1)任找一个人，其血可以输给小明的概率是多少？

    (2)任找一个人，其血不能输给小明的概率是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知△BCD中，∠BCD=90°，BC=CD=1，AB⊥平面BCD，∠ADB=60°，E、F分别是AC、AD上的动点，且

    （1）求证：不论为何值，总有平面BEF⊥平面ABC；

    （2）当λ为何值时，平面BEF⊥平面ACD ?

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某家电公司销售部门共有200位销售员，每位部门对每位销售员都有1400万元的年度销售任务，已知这200位销售员去年完成销售额都在区间（单位：百万元）内，现将其分成5组，第1组，第2组，第3组，第4组，第5组对应的区间分别为， ， ， ， ，绘制出频率分布直方图.

    （1）求的值，并计算完成年度任务的人数；

    （2）用分层抽样从这200位销售员中抽取容量为25的样本，求这5组分别应抽取的人数；

    （3）现从（2）中完成年度任务的销售员中随机选取2位，奖励海南三亚三日游，求获得此奖励的2位销售员在同一组的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知f（x）=sin2（π+x）﹣cos（2π﹣x）+a
    （1）求f（x）的值域
    （2）若f（x）在（0， ）内有零点，求a的范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列{an}的前n项和为Sn=﹣3n2+49n．
    （1）请问数列{an}是否为等差数列？如果是，请证明；
    （2）设bn=|an|，求数列{bn}的前n项和．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，△ABC和△BCD所在平面互相垂直，且AB=BC=BD=2．∠ABC=∠DBC=120°，E、F分别为AC、DC的中点．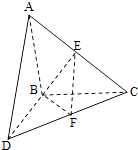

    （1）求证：EF⊥BC；
    （2）求二面角E﹣BF﹣C的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=Asin（ωx+φ）（A，ω＞0，﹣π＜φ＜π）在一个周期内的图象如图所示．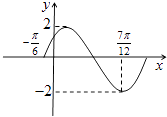

    （1）求f（x）的表达式；
    （2）在△ABC中，f（C+ ）=﹣1且 ＜0，求角C．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的离心率为，以原点为圆心，椭圆的短半轴长为半径的圆与直线x﹣y+=0相切．

    （Ⅰ）求椭圆C的方程；

    （Ⅱ）若过点M（2，0）的直线与椭圆C相交于两点A，B，当时，求直线斜率的取值范围．

    查看答案和解析>>

    同步练习册答案