考点:二次函数的性质
专题:函数的性质及应用
分析:若对于?x
1∈(1,+∞),?x
2∈(0,+∞)都有f(x
1)≥g(x
2)成立,即为:f(x
1)≥g(x
2)
min在x>1上恒成立,可先求出g(x)的最小值,再由
-1≤x2-5x+3-在x>1上恒成立.即为k≤(x-4)e
x在x>1上恒成立,令h(x)=(x-4)e
x运用导数求极小值,也是最小值,只要k不大于最小值,即可求得k的取值范围.
解答:
解:对于?x
1∈(1,+∞),?x
2∈(0,+∞)都有f(x
1)≥g(x
2)成立,
即为:f(x
1)≥g(x
2)
min在x>1上恒成立,对于g(x)=-x+xlnx
则:g′(x)=-1+lnx-1=lnx
令g′(x)>0,则x>1,g′(x)<0,则0<x<1
即在x=1为极小值且g(-1)=-1
则有
-1≤x2-5x+3-在x>1上恒成立,
即
≤x2-5x+4在x>1上恒成立,
即有k≤(x-4)e
x令h(x)=(x-4)e
x则:h′(x)=(x-3)e
x当x>3时,h′(x)>0,当1<x<3时,h′(x)<0
在x=3时,h(x)取极小值,即为最小值.h(3)=-e
3则有:k≤-e
3故选:B
点评:本题考查的知识要点:恒成立问题,函数的转化思想,利用函数的导数求函数的最值及相关的运算问题.



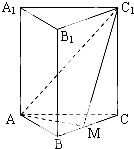 如图,正三棱柱ABC-A1B1C1的底面边长为1,点M在BC上,△AMC1是以M为直角顶点的等腰直角三角形.
如图,正三棱柱ABC-A1B1C1的底面边长为1,点M在BC上,△AMC1是以M为直角顶点的等腰直角三角形.