
【题目】已知定义域为![]() 的函数
的函数![]() 是奇函数.
是奇函数.
(1)求![]() ,判断函数
,判断函数![]() 的单调性并证明.
的单调性并证明.
(2)对任意的![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源: 题型:
【题目】如图,在边长为2的正方体ABCD-A1B1C1D1中,E是BC的中点,F是DD1的中点,

(1)求证:CF∥平面A1DE;
(2)求平面A1DE与平面A1DA夹角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列事件是随机事件的是( )
①当x>10时,![]() ; ②当x∈R,x2+x=0有解
; ②当x∈R,x2+x=0有解
③当a∈R关于x的方程x2+a=0在实数集内有解; ④当sinα>sinβ时,α>β( )
A.①②B.②③C.③④D.①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,某区有一块空地![]() ,其中
,其中![]() ,
,![]() ,
,![]() .当地区政府规划将这块空地改造成一个旅游景点,拟在中间挖一个人工湖
.当地区政府规划将这块空地改造成一个旅游景点,拟在中间挖一个人工湖![]() ,其中
,其中![]() 都在边
都在边![]() 上,且
上,且![]() ,挖出的泥土堆放在
,挖出的泥土堆放在![]() 地带上形成假山,剩下的
地带上形成假山,剩下的![]() 地带开设儿童游乐场.为安全起见,需在
地带开设儿童游乐场.为安全起见,需在![]() 的周围安装防护网.
的周围安装防护网.

(1)当![]() 时,求防护网的总长度;
时,求防护网的总长度;
(2)若要求挖人工湖用地![]() 的面积是堆假山用地
的面积是堆假山用地![]() 的面积的
的面积的![]() 倍,试确定
倍,试确定![]() 的大小;
的大小;
(3)为节省投入资金,人工湖![]() 的面积要尽可能小,问如何设计施工方案,可使
的面积要尽可能小,问如何设计施工方案,可使![]() 的面积最小?最小面积是多少?
的面积最小?最小面积是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面上一个圆可以将平面分成两个部分,两个圆最多可以将平面分成4个部分,设平面上![]() 个圆最多可以将平面分成
个圆最多可以将平面分成![]() 个部分.
个部分.
![]() 求
求![]() ,
,![]() 的值;
的值;
![]() 猜想
猜想![]() 的表达式并证明;
的表达式并证明;
![]() 证明:
证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题共13分)
已知![]() ,
, ![]() 或1,
或1, ![]()
![]() ,对于
,对于![]() ,
, ![]() 表示U和V中相对应的元素不同的个数.
表示U和V中相对应的元素不同的个数.
(Ⅰ)令![]() ,存在m个
,存在m个![]() ,使得
,使得![]() ,写出m的值;
,写出m的值;
(Ⅱ)令 ,若
,若![]() ,求证:
,求证: ![]() ;
;
(Ⅲ)令![]() ,若
,若![]() ,求所有
,求所有![]() 之和.
之和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() , (
, (![]() 为参数,
为参数, ![]() 为倾斜角).以坐标原点为极点,
为倾斜角).以坐标原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
(Ⅰ)将曲线![]() 的直角坐标方程化为极坐标方程;
的直角坐标方程化为极坐标方程;
(Ⅱ)设点![]() 的直角坐标为
的直角坐标为![]() ,直线
,直线![]() 与曲线
与曲线![]() 的交点为
的交点为![]() 、
、![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(I)![]() ;(II)
;(II)![]() .
.
【解析】试题分析:(Ⅰ)将由![]() 代入
代入![]() ,化简即可得到曲线
,化简即可得到曲线![]() 的极坐标方程;(Ⅱ)将
的极坐标方程;(Ⅱ)将![]() 的参数方程
的参数方程![]() 代入
代入![]() ,得
,得![]() ,根据直线参数方程的几何意义,利用韦达定理结合辅助角公式,由三角函数的有界性可得结果.
,根据直线参数方程的几何意义,利用韦达定理结合辅助角公式,由三角函数的有界性可得结果.
试题解析:(Ⅰ)由![]() 及
及![]() ,得
,得![]() ,即
,即![]()
所以曲线![]() 的极坐标方程为
的极坐标方程为![]()
(II)将![]() 的参数方程
的参数方程![]() 代入
代入![]() ,得
,得![]()
∴ , 所以
, 所以![]() ,又
,又![]() ,
,
所以![]() ,且
,且![]() ,
,
所以![]() ,
,
由![]() ,得
,得![]() ,所以
,所以![]() .
.
故![]() 的取值范围是
的取值范围是![]() .
.
【题型】解答题
【结束】
23
【题目】已知![]() 、
、![]() 、
、![]() 均为正实数.
均为正实数.
(Ⅰ)若![]() ,求证:
,求证: ![]()
(Ⅱ)若![]() ,求证:
,求证: ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校高三年级学生某次身体素质体能测试的原始成绩采用百分制,已知所有这些学生的原始成绩均分布在![]() 内,发布成绩使用等级制,各等级划分标准见下表.
内,发布成绩使用等级制,各等级划分标准见下表.
百分制 | 85分及以上 | 70分到84分 | 60分到69分 | 60分以下 |
等级 | A | B | C | D |
规定:A,B,C三级为合格等级,D为不合格等级为了解该校高三年级学生身体素质情况,从中抽取了n名学生的原始成绩作为样本进行统计.
按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的分组作出频率分布直方图如图1所示,样本中分数在80分及以上的所有数据的茎叶图如图2所示
的分组作出频率分布直方图如图1所示,样本中分数在80分及以上的所有数据的茎叶图如图2所示
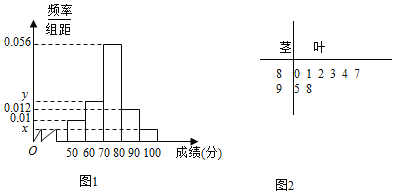
![]() 求n和频率分布直方图中的x,y的值,并估计该校高一年级学生成绩是合格等级的概率;
求n和频率分布直方图中的x,y的值,并估计该校高一年级学生成绩是合格等级的概率;
![]() 根据频率分布直方图,求成绩的中位数
根据频率分布直方图,求成绩的中位数![]() 精确到
精确到![]() ;
;
![]() 在选取的样本中,从A,D两个等级的学生中随机抽取2名学生进行调研,求至少有一名学生是A等级的概率.
在选取的样本中,从A,D两个等级的学生中随机抽取2名学生进行调研,求至少有一名学生是A等级的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】省环保厅对![]() 、
、![]() 、
、![]() 三个城市同时进行了多天的空气质量监测,测得三个城市空气质量为优或良的数据共有180个,三城市各自空气质量为优或良的数据个数如下表所示:
三个城市同时进行了多天的空气质量监测,测得三个城市空气质量为优或良的数据共有180个,三城市各自空气质量为优或良的数据个数如下表所示:
|
|
| |
优(个) | 28 |
|
|
良(个) | 32 | 30 |
|
已知在这180个数据中随机抽取一个,恰好抽到记录![]() 城市空气质量为优的数据的概率为0.2.
城市空气质量为优的数据的概率为0.2.
(1)现按城市用分层抽样的方法,从上述180个数据中抽取30个进行后续分析,求在![]() 城中应抽取的数据的个数;
城中应抽取的数据的个数;
(2)已知![]() ,
, ![]() ,求在
,求在![]() 城中空气质量为优的天数大于空气质量为良的天数的概率.
城中空气质量为优的天数大于空气质量为良的天数的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com