Question

7．已知点P为抛物线C：y²=4x上一点，记P到抛物线准线l的距离为d₁，点P到圆（x+2）²+（y+4）²=4的距离为d₂，则d₁+d₂的最小值是（　　）

• A． 6
• B． 1
• C． 5
• D． 3

Answer 1

分析 由抛物线定义知：P到准线距离等于P到焦点A的距离，连结圆心B与A，交圆于C，AB交抛物线的点即为使d₁+d₂最小时P的位置．由此能求出结果．

解答 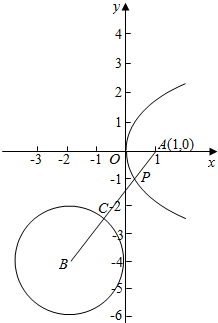解：∵点P是抛物线y²=4x上的点，
点P到抛物线的准线的距离为d₁，
P到圆（x+2）²+（y+4）²=4上的动点Q距离为d₂，
由抛物线定义知：P到准线距离等于P到焦点A的距离，
∴如图，连结圆心B与A，交圆于C，
AB交抛物线的点即为使d₁+d₂最小时P的位置．
∴（d₁+d₂）_min=|AC|，
∵B（-2，-4），A（1，0），
∴|AB|=$\sqrt{（-2-1）^{2}+（{-4-0）}^{2}}$=5．|BC|=2．
∴|AC|=5-2=3．
故选：D．

点评 本题考查与抛物线有关的两条线段和的最小值的求法，是中档题，解题时要熟练掌握抛物线性质．