【题目】对于函数①f（x）=4x+
-5，②f（x）=|log2 x|-（
）x，③f（x）=cos（x+2）-cosx，判断如下两个命题的真假：
命题甲：f（x）在区间（1，2）上是增函数；
命题乙：f（x）在区间（0，+∞）上恰有两个零点x1，x2，且x1x2<1.
能使命题甲、乙均为真的函数的序号是_____________.
【答案】
【解析】①
,在区间（1，2）上
, 
在区间（1，2）上是增函数,使甲为真,f(x)的最小值是
,又
,
在
上恰有两个零点: 
, 使乙为真; ②在区间（1，2）上, 
,是增函数, 
也是增函数,两者的和函数
也是增函数,使甲为真.分别画出
与
的图象,恰有两个不同的交点,即
在区间（0，+∞）上恰有两个零点x1，x2,且
,使乙为真; ③令
,可得: 
即
,在区间（0，+∞）上有无数个零点,使乙为假;综上可知,应填①②.
点睛:对于函数
,我们把使
的实数x叫做函数
的零点, 函数
的零点就是方程
的实数根,也是函数
的图象与x轴的交点的横坐标.如果函数
在区间
上的图象是连续不断的一条曲线,并且有
,那么函数
在区间
内有零点,即存在
,使得
,这个c也就是方程
的根.
新题型全程检测期末冲刺100分系列答案科目：高中数学 来源： 题型：
【题目】如图，椭圆
的上、下顶点分别为
， 
，右焦点为
，点
在椭圆
上，且
.
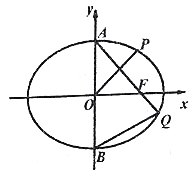
（1）若点
坐标为
，求椭圆
的方程；
（2）延长
交椭圆
与点
，若直线
的斜率是直线
的斜率的3倍，求椭圆
的离心率；
（3）是否存在椭圆
，使直线
平分线段
？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某公司对新研发的一种产品进行试销，得到如下数据及散点图：
其中
， 
， 
， 
.
（1）根据散点图判断
与
， 
与
哪一对具有较强的线性相关性（给出判断即可，不必说明理由）？
（2）根据（1）的判断结果及数据，建立
关于
的回归方程（运算过程及回归方程中的系数均保留两位有效数字）.
（3）定价为150元/ 
时，天销售额的预报值为多少元？
附：对于一组数据
，其回归直线
的斜率和截距的最小二乘法估计分别为
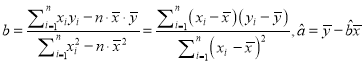
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
（
， 
）为奇函数，且相邻两对称轴间的距离为
.
（1）当
时，求
的单调递减区间；
（2）将函数
的图象沿
轴方向向右平移
个单位长度，再把横坐标缩短到原来的
（纵坐标不变），得到函数
的图象.当
时，求函数
的值域.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f(x)＝x3－3ax－1，a≠0.
(1)求f(x)的单调区间；
(2)若f(x)在x＝－1处取得极值，直线y＝m与y＝f(x)的图象有三个不同的交点，求m的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图,椭圆
(
)的离心率是
,过点
(
,
)的动直线
与椭圆相交于
,
两点,当直线平行于
轴时,直线被椭圆截得的线段长为
．
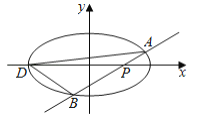
⑴求椭圆的方程:
⑵已知
为椭圆的左端点,问: 是否存在直线使得
的面积为
?若不存在,说明理由,若存在,求出直线的方程．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
