
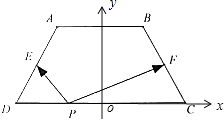
【题目】如图,在等腰梯形ABCD中,AB=2,CD=4,BC= ![]() ,点E,F分别为AD,BC的中点.如果对于常数λ,在ABCD的四条边上,有且只有8个不同的点P使得
,点E,F分别为AD,BC的中点.如果对于常数λ,在ABCD的四条边上,有且只有8个不同的点P使得 ![]() =λ成立,那么实数λ的取值范围为 .
=λ成立,那么实数λ的取值范围为 . 
【答案】(﹣ ![]() ,﹣
,﹣ ![]() )
)
【解析】解:以DC所在直线为x轴,DC的中垂线为y轴建立平面直角坐标系,
则梯形的高为 ![]() =2,∴A(﹣1,2),B(1,2),C(2,0),D(﹣2,0),∴E(﹣
=2,∴A(﹣1,2),B(1,2),C(2,0),D(﹣2,0),∴E(﹣ ![]() ,1),F(
,1),F( ![]() ,1).
,1).
①当P在DC上时,设P(x,0)(﹣2≤x≤2),则 ![]() =(﹣
=(﹣ ![]() ﹣x,1)
﹣x,1) ![]() =(
=( ![]() ,1).
,1).
于是 ![]() =(﹣
=(﹣ ![]() ﹣x)(
﹣x)( ![]() ﹣x)+1=x2﹣
﹣x)+1=x2﹣ ![]() =λ,
=λ,
∴当λ=﹣ ![]() 时,方程有一解,当﹣
时,方程有一解,当﹣ ![]() <λ≤
<λ≤ ![]() 时,λ有两解;
时,λ有两解;
②当P在AB上时,设P(x,2)(﹣1≤x≤1),则 ![]() =(﹣
=(﹣ ![]() ﹣x,﹣1)
﹣x,﹣1) ![]() =(
=( ![]() ,﹣1).
,﹣1).
于是 ![]() =(﹣
=(﹣ ![]() ﹣x)(
﹣x)( ![]() ﹣x)+1=x2﹣
﹣x)+1=x2﹣ ![]() =λ,
=λ,
∴当λ=﹣ ![]() 时,方程有一解,当﹣
时,方程有一解,当﹣ ![]() <λ≤﹣
<λ≤﹣ ![]() 时,λ有两解;
时,λ有两解;
③当P在AD上时,直线AD方程为y=2x+4,
设P(x,2x+4)(﹣2<x<﹣1),则 ![]() =(﹣
=(﹣ ![]() ﹣x,﹣2x﹣3)
﹣x,﹣2x﹣3) ![]() =(
=( ![]() ,﹣2x﹣3).
,﹣2x﹣3).
于是 ![]() =(﹣
=(﹣ ![]() ﹣x)(
﹣x)( ![]() ﹣x)+(﹣2x﹣3)2=5x2+12x+
﹣x)+(﹣2x﹣3)2=5x2+12x+ ![]() =λ.
=λ.
∴当λ=﹣ ![]() 或﹣
或﹣ ![]() <λ<
<λ< ![]() 时,方程有一解,当﹣
时,方程有一解,当﹣ ![]() ﹣
﹣ ![]() 时,方程有两解;
时,方程有两解;
④当P在BC上时,直线BC的方程为y=﹣2x+4,
设P(x,﹣2x+4)(1<x<2),则 ![]() =(﹣
=(﹣ ![]() ﹣x,2x﹣3)
﹣x,2x﹣3) ![]() =(
=( ![]() ,2x﹣3).
,2x﹣3).
于是 ![]() =(﹣
=(﹣ ![]() ﹣x)(
﹣x)( ![]() ﹣x)+(2x﹣3)2=5x2﹣12x+
﹣x)+(2x﹣3)2=5x2﹣12x+ ![]() =λ.
=λ.
∴当λ=﹣ ![]() 或﹣
或﹣ ![]() <λ<
<λ< ![]() 时,方程有一解,当﹣
时,方程有一解,当﹣ ![]() ﹣
﹣ ![]() 时,方程有两解;
时,方程有两解;
综上,若使梯形上有8个不同的点P满足 ![]() =λ成立,
=λ成立,
则λ的取值范围是(﹣ ![]() ,
, ![]() ]∩(﹣
]∩(﹣ ![]() ,﹣
,﹣ ![]() ]∩(﹣
]∩(﹣ ![]() ,﹣
,﹣ ![]() )∩(﹣
)∩(﹣ ![]() ,﹣
,﹣ ![]() )=(﹣
)=(﹣ ![]() ,﹣
,﹣ ![]() ).
).
所以答案是:(﹣ ![]() ,﹣
,﹣ ![]() ).
).


 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:高中数学 来源: 题型:
【题目】下列说法正确的是 ( )
A. “x<1”是“log2(x+1)<1”的充分不必要条件
B. 命题“x>0,2x>1”的否定是“x0≤0,![]() ≤1”
≤1”
C. 命题“若a≤b,则ac2≤bc2”的逆命题是真命题
D. 命题“若a+b≠5,则a≠2或b≠3”的逆否命题为真命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲,乙两人进行围棋比赛,共比赛2n(n∈N+)局,根据以往比赛胜负的情况知道,每局甲胜的概率和乙胜的概率均为 ![]() .如果某人获胜的局数多于另一人,则此人赢得比赛.记甲赢得比赛的概率为P(n).
.如果某人获胜的局数多于另一人,则此人赢得比赛.记甲赢得比赛的概率为P(n).
(1)求P(2)与P(3)的值;
(2)试比较P(n)与P(n+1)的大小,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an},{bn}均为各项都不相等的数列,Sn为{an}的前n项和,an+1bn=Sn+1(n∈N).
(1)若a1=1,bn= ![]() ,求a4的值;
,求a4的值;
(2)若{an}是公比为q的等比数列,求证:存在实数λ,使得{bn+λ}为等比数列;
(3)若{an}的各项都不为零,{bn}是公差为d的等差数列,求证:a2 , a3 , …,an…成等差数列的充要条件是d= ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲,乙两人进行围棋比赛,共比赛2n(n∈N+)局,根据以往比赛胜负的情况知道,每局甲胜的概率和乙胜的概率均为 ![]() .如果某人获胜的局数多于另一人,则此人赢得比赛.记甲赢得比赛的概率为P(n).
.如果某人获胜的局数多于另一人,则此人赢得比赛.记甲赢得比赛的概率为P(n).
(1)求P(2)与P(3)的值;
(2)试比较P(n)与P(n+1)的大小,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为评估设备![]() 生产某种零件的性能,从设备
生产某种零件的性能,从设备![]() 生产零件的流水线上随机抽取100件零件作为样本,测量其直径后,整理得到下表:
生产零件的流水线上随机抽取100件零件作为样本,测量其直径后,整理得到下表:
直径mm | 58 | 59 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 73 | 合计 |
件数 | 1 | 1 | 3 | 5 | 6 | 19 | 33 | 18 | 4 | 4 | 2 | 1 | 2 | 1 | 100 |
经计算,样本的平均值![]() ,标准差
,标准差![]() ,以频率值作为概率的估计值.
,以频率值作为概率的估计值.
(1)为评判一台设备的性能,从该设备加工的零件中任意抽取一件,记其直径为![]() ,并根据以下不等式进
,并根据以下不等式进
行评判(![]() 表示相应事件的概率);①
表示相应事件的概率);①![]() ;②
;②![]() ;③
;③![]() .
.
评判规则为:若同时满足上述三个不等式,则设备等级为甲;仅满足其中两个,则等级为乙;若仅满足其中一个,则等级为丙;若全部不满足,则等级为丁,试判断设备![]() 的性能等级.
的性能等级.
(2)将直径小于等于![]() 或直径大于
或直径大于![]() 的零件认为是次品.
的零件认为是次品.
(ⅰ)从设备![]() 的生产流水线上随意抽取2件零件,计算其中次品个数
的生产流水线上随意抽取2件零件,计算其中次品个数![]() 的数学期望
的数学期望![]() ;
;
(ⅱ)从样本中随意抽取2件零件,计算其中次品个数![]() 的数学期望
的数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在等腰梯形ABCD中,AB=2,CD=4,BC= ![]() ,点E,F分别为AD,BC的中点.如果对于常数λ,在ABCD的四条边上,有且只有8个不同的点P使得
,点E,F分别为AD,BC的中点.如果对于常数λ,在ABCD的四条边上,有且只有8个不同的点P使得 ![]() =λ成立,那么实数λ的取值范围为 .
=λ成立,那么实数λ的取值范围为 . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,A,B,C的对边分别是a,b,c,3sin2C+8sin2A=11sinAsinC,且c<2a.
(1)求证:△ABC为等腰三角形
(2)若△ABC的面积为8 ![]() .且sinB=
.且sinB= ![]() ,求BC边上的中线长.
,求BC边上的中线长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com