
 x2,实数p,q满足p2-4q≥0,x1,x2是方程x2-px+q=0的两根,记φ(p,q)=max{|x1|,|x2|}.
x2,实数p,q满足p2-4q≥0,x1,x2是方程x2-px+q=0的两根,记φ(p,q)=max{|x1|,|x2|}.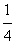 p0)(p0≠0)作L的切线教y轴于点B。证明:对线段AB上任一点Q(p,q)有φ(p,q)=
p0)(p0≠0)作L的切线教y轴于点B。证明:对线段AB上任一点Q(p,q)有φ(p,q)= ;
; p12),E′(p2,
p12),E′(p2, p22),l1,l2与y轴分别交与F,F'。线段EF上异于两端点的点集记为X。证明:M(a,b)∈X
p22),l1,l2与y轴分别交与F,F'。线段EF上异于两端点的点集记为X。证明:M(a,b)∈X |P1|>|P2|
|P1|>|P2| φ(a,b)=
φ(a,b)=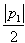 ;
; (x+1)2-
(x+1)2- },当点(p,q)取遍D时,求φ(p,q)的最小值 (记为φmin)和最大值(记为φmax)。
},当点(p,q)取遍D时,求φ(p,q)的最小值 (记为φmin)和最大值(记为φmax)。科目:高中数学 来源: 题型:
| 1 |
| 4 |
| 1 |
| 4 |
| |p0| |
| 2 |
| 1 |
| 4 |
| p | 2 1 |
| 1 |
| 4 |
| |p1| |
| 2 |
| 1 |
| 4 |
| 5 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
| OA |
| OM |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
| 2 |
| 1 |
| 2 |
| OM |
| OA |
2
| ||
| 2 |
2
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
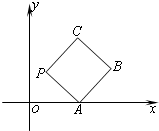 (2012•浦东新区一模)如图所示,在平面直角坐标系xOy上放置一个边长为1的正方形PABC,此正方形PABC沿x轴滚动(向左或向右均可),滚动开始时,点P位于原点处,设顶点P(x,y)的纵坐标与横坐标的函数关系是y=f(x),x∈R,该函数相邻两个零点之间的距离为m.
(2012•浦东新区一模)如图所示,在平面直角坐标系xOy上放置一个边长为1的正方形PABC,此正方形PABC沿x轴滚动(向左或向右均可),滚动开始时,点P位于原点处,设顶点P(x,y)的纵坐标与横坐标的函数关系是y=f(x),x∈R,该函数相邻两个零点之间的距离为m.| 函数性质 | 结 论 | |
| 奇偶性 | 偶函数 偶函数 | |
| 单调性 | 递增区间 | [4k,4k+2],k∈z [4k,4k+2],k∈z |
| 递减区间 | [4k-2,4k],k∈z [4k-2,4k],k∈z | |
| 零点 | x=4k,k∈z x=4k,k∈z | |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com