
四名教师被分到甲、乙、丙三所学校参加工作,每所学校至少一名教师.
(Ⅰ)求 、
、 两名教师被同时分配到甲学校的概率;
两名教师被同时分配到甲学校的概率;
(Ⅱ)求 、
、 两名教师不在同一学校的概率;
两名教师不在同一学校的概率;
(Ⅲ)设随机变量 为这四名教师中分配到甲学校的人数,求
为这四名教师中分配到甲学校的人数,求 的分布列和数学期望.
的分布列和数学期望.
(Ⅰ) ;
;
(Ⅱ) 、
、 两名教师不在同一学校的概率
两名教师不在同一学校的概率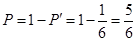 ;
;
(Ⅲ)以随机变量 的分布列为
的分布列为
1 2 
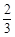
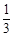
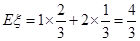 。
。
解析试题分析:(Ⅰ)四名教师被分到甲、乙、丙三所学校的所有可能情况为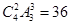 种 1分
种 1分 、
、 两名教师被同时分配到甲学校的情况为
两名教师被同时分配到甲学校的情况为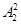
所以 、
、 两名教师被同时分配到甲学校的概率为
两名教师被同时分配到甲学校的概率为 5分
5分
(Ⅱ) 、
、 两名教师被分在同一学校的概率为
两名教师被分在同一学校的概率为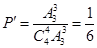
所以 、
、 两名教师不在同一学校的概率
两名教师不在同一学校的概率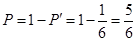 9分
9分
(Ⅲ)随机变量 的可取值为1,2
的可取值为1,2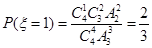
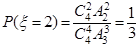
所以随机变量 的分布列为
的分布列为
1 2 
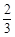
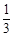
(不列表不扣分) 11分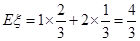 13分
13分
考点:简单排列组合应用问题,古典概型概率的计算,随机变量的分布列及其数学期望。
点评:中档题,本题综合性较强,为计算概率,需要应用排列组合知识,对分析问题解决问题的能力要求较高。利用对立事件的概率计算公式,往往可简化解题过程。


科目:高中数学 来源: 题型:解答题
甲、乙两人玩猜数字游戏,规则如下:
①连续竞猜 次,每次相互独立;
次,每次相互独立;
②每次竟猜时,先由甲写出一个数字,记为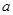 ,再由乙猜测甲写的数字,记为
,再由乙猜测甲写的数字,记为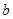 ,已知
,已知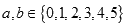 ,若
,若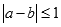 ,则本次竞猜成功;
,则本次竞猜成功;
③在 次竞猜中,至少有
次竞猜中,至少有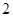 次竞猜成功,则两人获奖.
次竞猜成功,则两人获奖.
(Ⅰ) 求甲乙两人玩此游戏获奖的概率;
(Ⅱ)现从 人组成的代表队中选
人组成的代表队中选 人参加此游戏,这
人参加此游戏,这 人中有且仅有
人中有且仅有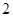 对双胞胎,记选出的
对双胞胎,记选出的 人中含有双胞胎的对数为
人中含有双胞胎的对数为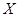 ,求
,求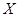 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
袋中有红、黄、白三种颜色的球各一个,从中每次取一只,有放回的抽取三次,
求:(1)3只球颜色全相同的概率;
(2)3只球颜色不全相同的概率;
(3)3只球颜色全不相同的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
数学试题中有12道单项选择题,每题有4个选项。某人对每道题都随机选其
中一个答案(每个选项被选出的可能性相同),求答对多少题的概率最大?并求出此种情况下概
率的大小.(可保留运算式子)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某医院将一专家门诊已诊的1000例病人的病情及诊断所用时间(单位:分钟)进行了统计,如下表.若视频率为概率,请用有关知识解决下列问题.
| 病症及代号 | 普通病症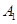 | 复诊病症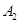 | 常见病症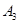 | 疑难病症 | 特殊病症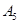 |
| 人数 | 100 | 300 | 200 | 300 | 100 |
| 每人就诊时间(单位:分钟) | 3 | 4 | 5 | 6 | 7 |
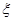 表示某病人诊断所需时间,求
表示某病人诊断所需时间,求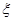 的数学期望.
的数学期望.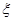 ,求
,求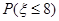 ;
;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
下表是我国2010年和2011年2~6月CPI同比(即当年某月与前一年同月相比)的增长数据,其中2011年的5个CPI数据成等差数列.
(Ⅰ)求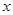 、
、 、
、 的值;
的值;
(Ⅱ)求2011年2~6月我国CPI数据的方差;
(Ⅲ)一般认为,某月CPI数据达到或超过3个百分点就已经通货膨胀,而达到或超过5个百分点为严重通货膨胀,现随机从2010年5个月和2011年5个月的数据中各抽取一个数据,求相同月份2010年通货膨胀,并且2011年严重通货膨胀的概率.
我国2010年和2011年2~6月份的CPI数据(单位:百分点,1个百分点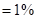 )
)
| 年份 | 二月 | 三月 | 四月 | 五月 | 六月 |
| 2010 | 2.7 | 2.4 | 2.8 | 3.1 | 3.9 |
| 2011 | 4.9 | 5.0 | 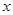 |  |  |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
一汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆):
| | 轿车A | 轿车B | 轿车C |
| 舒适型 | 100 | 150 | z |
| 标准型 | 300 | 450 | 600 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某项选拔共有三轮考核,每轮设有一个问题,能正确回答问题者进入下一轮考试,否则即被淘汰,已知某选手能正确回答第一、二、三轮的问题的概率分别为 且各轮问题能否正确回答互不影响.
且各轮问题能否正确回答互不影响.
(Ⅰ)求该选手被淘汰的概率;
(Ⅱ)该选手在选拔中回答问题的个数记为ξ,求随机变量ξ的分布列与数学期望.
(注:本小题结果可用分数表示)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某商家举办购物抽奖活动,盒中有大小相同的9张卡片,其中三张标有数字1,两张标有数字0,四张标有数字 ,先从中任取三张卡片,将卡片上的数字相加,设数字和为
,先从中任取三张卡片,将卡片上的数字相加,设数字和为 ,当
,当 时,奖励奖金
时,奖励奖金 元;当
元;当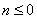 时,无奖励.
时,无奖励.
(1)求取出的三个数字中恰有一个 的概率.
的概率.
(2)设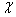 为奖金金额,求
为奖金金额,求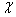 的分布列和期望.
的分布列和期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com