
【题目】如图1,已知长方形ABCD中,AB=2,AD=1,E为DC的中点.将△ADE沿AE折起,使得平面ADE⊥平面ABCE. 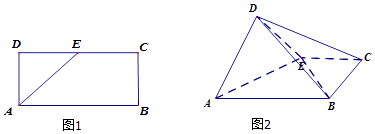
(1)求证:平面BDE⊥平面ADE
(2)求三棱锥 C﹣BDE的体积
【答案】
(1)证明:连接BE,∵长方形ABCD中,AB=2,AD=1,
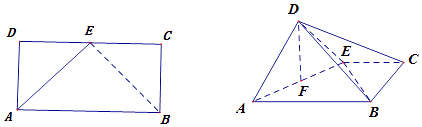
E为DC的中点,DE=1,∴AE=BE= ![]()
∴AE2+BE2=2=AB2,∴BE⊥AE.
∵平面ADE⊥平面ABCE,平面ADE∩平面ABCE=AE,BE平面ABCE
∴BE⊥平面ADE,又∵BE平面BDE,
∴平面BDE⊥平面ADE.
(2)解:取AE中点F,连结DF,
∵AD=DE,∴DF⊥AE,
又∵平面ADE⊥平面ABCE,且交线为AE,DF平面ADE,
∴DF⊥平面BCE
在Rt△ADE中,AD=DE=1,AE= ![]() ,∴DF=
,∴DF= ![]() ,
,
∴ ![]()
又∵VC﹣BED=VD﹣BCE,
∴三棱锥C﹣BDE的体积 ![]()
【解析】(1)连接BE,推民出BE⊥AE,从而BE⊥平面ADE,由此能证明平面BDE⊥平面ADE.(2)取AE中点F,连结DF,由VC﹣BED=VD﹣BCE,能求出三棱锥C﹣BDE的体积.
【考点精析】通过灵活运用平面与平面垂直的判定,掌握一个平面过另一个平面的垂线,则这两个平面垂直即可以解答此题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知四棱锥P﹣ABCD的正视图1是一个底边长为4、腰长为3的等腰三角形,图2、图53分别是四棱锥P﹣ABCD的侧视图和俯视图. 
(1)求证:AD⊥PC;
(2)求四棱锥P﹣ABCD的侧面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:9x2+y2=m2(m>0),直线l不过原点O且不平行于坐标轴,l与C有两个交点A,B,线段AB的中点为M.
(1)证明:直线OM的斜率与l的斜率的乘积为定值;
(2)若l过点( ![]() ,m),延长线段OM与C交于点P,四边形OAPB能否为平行四边形?若能,求此时l的斜率;若不能,说明理由.
,m),延长线段OM与C交于点P,四边形OAPB能否为平行四边形?若能,求此时l的斜率;若不能,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系x0y中,已知点A(﹣ ![]() ,0),B(
,0),B( ![]() ),E为动点,且直线EA与直线EB的斜率之积为﹣
),E为动点,且直线EA与直线EB的斜率之积为﹣ ![]() . (Ⅰ)求动点E的轨迹C的方程;
. (Ⅰ)求动点E的轨迹C的方程;
(Ⅱ)设过点F(1,0)的直线l与曲线C相交于不同的两点M,N.若点P在y轴上,且|PM|=|PN|,求点P的纵坐标的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(0,﹣2),椭圆E: ![]() +
+ ![]() =1(a>0,b>0)的离心率为
=1(a>0,b>0)的离心率为 ![]() ,F是椭圆E的右焦点,直线AF的斜率为
,F是椭圆E的右焦点,直线AF的斜率为 ![]() ,O是坐标原点.
,O是坐标原点.
(1)求E的方程;
(2)设过点A的直线l与E相交于P,Q两点,当△OPQ的面积最大时,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,底面ABCD是边长为2的菱形,∠BAD=60°,PD⊥底面ABCD,点M、N分别是棱AB、CD的中点. 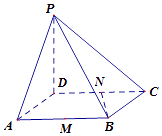
(1)证明:BN⊥平面PCD;
(2)在线段PC上是否存在点H,使得MH与平面PCD所成最大角的正切值为 ![]() ,若存在,请求出H点的位置;若不存在,请说明理由.
,若存在,请求出H点的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)是定义在R上的偶函数,对任意x∈R,都有f(x)=f(x+4),且当x∈[﹣2,0]时,f(x)=( ![]() )x﹣1,若在区间(﹣2,6]内关于x的方程f(x)﹣loga(x+2)=0(a>1)恰有三个不同的实数根,则a的取值范围是( )
)x﹣1,若在区间(﹣2,6]内关于x的方程f(x)﹣loga(x+2)=0(a>1)恰有三个不同的实数根,则a的取值范围是( )
A.( ![]() ,2)
,2)
B.( ![]() ,2)
,2)
C.[ ![]() ,2)
,2)
D.( ![]() ,2]
,2]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com