
【题目】已知等差数列![]() 满足
满足![]() ,
,![]() .
.
(1)求![]() 的通项公式;
的通项公式;
(2)若![]() ,数列
,数列![]() 满足关系式
满足关系式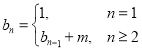 ,求证:数列
,求证:数列![]() 的通项公式为
的通项公式为![]() ;
;
(3)设(2)中的数列![]() 的前n项和为
的前n项和为![]() ,对任意的正整数n,
,对任意的正整数n,![]() 恒成立,求实数p的取值范围.
恒成立,求实数p的取值范围.
【答案】(1)![]() ,
,![]() ;(2)见解析;(3)
;(2)见解析;(3)![]()
【解析】
(1)由等差数列由通项公式,得到首项与公差的方程组,得出首项与公差的值,得到通项公式;
(2)已知数列的递推公式,由叠加法,得到数列的通项公式;
(3)将数列求和得到前n项和后,将条件变形后,得到关于参数p的关系式,这是一个恒成立问题,通过最值的研究,得到本题结论.
(1)设等差数列![]() 的公差为d,
的公差为d,
由已知,有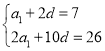 ,
,
解得![]()
所以![]() ,
,
即等差数列![]() 的通项公式为
的通项公式为![]() ,
,![]() .
.
(2)因为![]() ,
,
所以,当![]() 时,
时,![]() .
.
证法一(数学归纳法):
①当![]() 时,
时,![]() ,结论成立;
,结论成立;
②假设当![]() 时结论成立,即
时结论成立,即![]() ,
,
那么当![]() 时,
时,![]() ,
,
即![]() 时,结论也成立.
时,结论也成立.
由①,②得,当![]() 时,
时,![]() 成立.
成立.
证法二:当![]() 时,
时,![]() ,
,
所以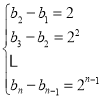
将这![]() 个式子相加,得
个式子相加,得![]() ,
,
即![]() .
.
当![]() 时,
时,![]() 也满足上式.
也满足上式.
所以数列![]() 的通项公式为
的通项公式为![]() .
.
(3)由(2)![]() ,所以
,所以![]() ,
,
![]() 原不等式变为
原不等式变为![]() ,即
,即![]() ,
,
![]() 对任意
对任意![]() 恒成立,
恒成立,
![]() 为任意的正整数,
为任意的正整数,
![]() .
.
![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】为了更好地支持“中小型企业”的发展,某市决定对部分企业的税收进行适当的减免,某机构调查了当地的中小型企业年收入情况,并根据所得数据画出了样本的频率分布直方图,下面三个结论:
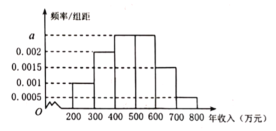
①样本数据落在区间![]() 的频率为0.45;
的频率为0.45;
②如果规定年收入在500万元以内的企业才能享受减免税政策,估计有55%的当地中小型企业能享受到减免税政策;
③样本的中位数为480万元.
其中正确结论的个数为( )
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】冬季历来是交通事故多发期,面临着货运高危运行、恶劣天气频发、包车客运监管漏洞和农村交通繁忙等四个方面的挑战.全国公安交管部门要认清形势、正视问题,针对近期事故暴露出来的问题,强薄羽、补短板、堵漏洞,进一步推动五大行动,巩固扩大五大行动成果,全力确保冬季交通安全形势稳定.据此,某网站推出了关于交通道路安全情况的调查,通过调查年龄在![]() 的人群,数据表明,交通道路安全仍是百姓最为关心的热点,参与调查者中关注此类问题的约占80%,现从参与调查并关注交通道路安全的人群中随机选出100人,并将这100人按年龄分组:第1组
的人群,数据表明,交通道路安全仍是百姓最为关心的热点,参与调查者中关注此类问题的约占80%,现从参与调查并关注交通道路安全的人群中随机选出100人,并将这100人按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
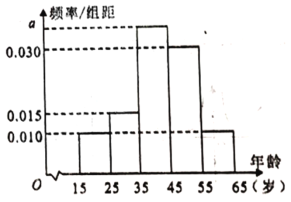
(1)求这100人年龄的样本平均数(同一组数据用该区间的中点值作代表)和中位数(精确到小数点后一位);
(2)现在要从年龄较大的第4,5组中用分层抽样的方法抽取8人,再从这8人中随机抽取3人进行问卷调查,求第4组恰好抽到2人的概率;
(3)若从所有参与调查的人(人数很多)中任意选出3人,设其中关注交通道路安全的人数为随机变量X,求X的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定数列![]() ,记该数列前
,记该数列前![]() 项
项![]() 中的最大项为
中的最大项为![]() ,即
,即![]() ,该数列后
,该数列后![]() 项
项![]() 中的最小项为
中的最小项为![]() ,记
,记![]() ,
,![]() ;
;
(1)对于数列:3,4,7,1,求出相应的![]() ,
,![]() ,
,![]() ;
;
(2)若![]() 是数列
是数列![]() 的前
的前![]() 项和,且对任意
项和,且对任意![]() ,有
,有![]() ,其中
,其中![]() 为实数,
为实数,![]() 且
且![]() ,
,![]() .
.
(ⅰ)设![]() ,证明:数列
,证明:数列![]() 是等比数列;
是等比数列;
(ⅱ)若数列![]() 对应的
对应的![]() 满足
满足![]() 对任意的正整数
对任意的正整数![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
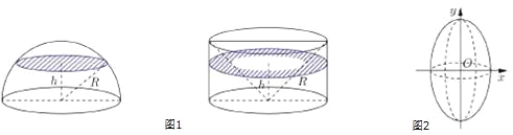
【题目】(数学文卷·2017届重庆十一中高三12月月考第16题) 现介绍祖暅原理求球体体积公式的做法:可构造一个底面半径和高都与球半径相等的圆柱,然后在圆柱内挖去一个以圆柱下底面圆心为顶点,圆柱上底面为底面的圆锥,用这样一个几何体与半球应用祖暅原理(图1),即可求得球的体积公式.请研究和理解球的体积公式求法的基础上,解答以下问题:已知椭圆的标准方程为![]() ,将此椭圆绕y轴旋转一周后,得一橄榄状的几何体(图2),其体积等于______.
,将此椭圆绕y轴旋转一周后,得一橄榄状的几何体(图2),其体积等于______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左焦点为
的左焦点为![]() ,经过点
,经过点![]() 的直线与椭圆相交于
的直线与椭圆相交于![]() ,
,![]() 两点,点
两点,点![]() 为线段
为线段![]() 的中点,点
的中点,点![]() 为坐标原点.当直线
为坐标原点.当直线![]() 的斜率为
的斜率为![]() 时,直线
时,直线![]() 的斜率为
的斜率为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若点![]() 为椭圆的左顶点,点
为椭圆的左顶点,点![]() 为椭圆的右顶点,过
为椭圆的右顶点,过![]() 的动直线交该椭圆于
的动直线交该椭圆于![]() ,
,![]() 两点,记
两点,记![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在坐标原点,且经过点
的中心在坐标原点,且经过点![]() ,它的一个焦点与抛物线E:
,它的一个焦点与抛物线E:![]() 的焦点重合,斜率为k的直线l交抛物线E于A、B两点,交椭圆
的焦点重合,斜率为k的直线l交抛物线E于A、B两点,交椭圆![]() 于C、D两点.
于C、D两点.
(1)求椭圆![]() 的方程;
的方程;
(2)直线l经过点![]() ,设点
,设点![]() ,且
,且![]() 的面积为
的面积为![]() ,求k的值;
,求k的值;
(3)若直线l过点![]() ,设直线
,设直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() 成等差数列,求直线l的方程.
成等差数列,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 和
和![]() 是双曲线
是双曲线![]() 上的两点,线段
上的两点,线段![]() 的中点为
的中点为![]() ,直线
,直线![]() 不经过坐标原点
不经过坐标原点![]() .
.
(1)若直线![]() 和直线
和直线![]() 的斜率都存在且分别为
的斜率都存在且分别为![]() 和
和![]() ,求证:
,求证:![]() ;
;
(2)若双曲线的焦点分别为![]() 、
、![]() ,点
,点![]() 的坐标为
的坐标为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,求由四点
,求由四点![]() 、
、![]() 、
、![]() 、
、![]() 所围成四边形
所围成四边形![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com