
【题目】某单位用2160万元购得一块空地,计划在该地块上建造一栋至少10层,每层2000平方米的楼房.经测算,如果将楼房建为x(x≥10)层,则每平方米的平均建筑费用为560+48x(单位:元).
(1)写出楼房平均综合费用y关于建造层数x的函数关系式;
(2)该楼房应建造多少层时,可使楼房每平方米的平均综合费用最少?最少值是多少?
【答案】解:(1)设楼房每平方米的平均综合费为y元,依题意得
y=(560+48x)+![]() =560+48x+
=560+48x+![]() (x≥10,x∈N*);
(x≥10,x∈N*);
(定义域不对扣1﹣2分)
(2)法一:∵x>0,∴48x+![]() ≥2
≥2![]() =1440,
=1440,
当且仅当48x=![]() ,即x=15时取到“=”,
,即x=15时取到“=”,
此时,平均综合费用的最小值为560+1440=2000元.
答:当该楼房建造15层,可使楼房每平方米的平均综合费用最少,最少值为2000元.
【解析】(1)由已知得,楼房每平方米的平均综合费为每平方米的平均建筑费用为560+48x与平均地皮费用的和,由已知中某单位用2160万元购得一块空地,计划在该地块上建造一栋x层,每层2000平方米的楼房,我们易得楼房平均综合费用y关于建造层数x的函数关系式;
(2)由(1)中的楼房平均综合费用y关于建造层数x的函数关系式,要求楼房每平方米的平均综合费用最小值,我们有两种思路,一是利用基本不等式,二是使用导数法,分析函数的单调性,再求最小值.


科目:高中数学 来源: 题型:
【题目】已知圆![]() :
: ![]() (
(![]() ),设
),设![]() 为圆
为圆![]() 与
与![]() 轴负半轴的交点,过点
轴负半轴的交点,过点![]() 作圆
作圆![]() 的弦
的弦![]() ,并使弦
,并使弦![]() 的中点恰好落在
的中点恰好落在![]() 轴上.
轴上.
(Ⅰ)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)延长![]() 交曲线
交曲线![]() 于点
于点![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 交于点
交于点![]() ,试判断以点
,试判断以点![]() 为圆心,线段
为圆心,线段![]() 长为半径的圆与直线
长为半径的圆与直线![]() 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l过点A(﹣3,4)
(1)若l与直线y=﹣2x+5平行,求其一般式方程;
(2)若l与直线y=﹣2x+5垂直,求其一般式方程;
(3)若l与两个坐标轴的截距之和等于12,求其一般式方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】命题![]() :已知实数
:已知实数![]() ,
, ![]() 满足约束条件
满足约束条件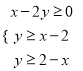 ,二元一次不等式
,二元一次不等式![]() 恒成立,
恒成立,
命题![]() :设数列
:设数列![]() 的通项公式为
的通项公式为![]() ,若
,若![]() ,使得
,使得![]() .
.
(1)分别求出使命题![]() ,
, ![]() 为真时,实数
为真时,实数![]() 的取值范围;
的取值范围;
(2)若命题![]() 与
与![]() 真假相同,求实数
真假相同,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,若直线
轴正半轴为极轴,建立极坐标系,若直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数, ![]() 为
为![]() 的倾斜角),曲线
的倾斜角),曲线![]() 的极坐标方程为
的极坐标方程为![]() ,射线
,射线![]() ,
, ![]() ,
, ![]() 与曲线
与曲线![]() 分别交于不同于极点的三点
分别交于不同于极点的三点![]() .
.
(1)求证: ![]() ;
;
(2)当![]() 时,直线
时,直线![]() 过
过![]() 两点,求
两点,求![]() 与
与![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市计划销售某种产品,先试销该产品![]() 天,对这
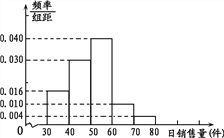
天,对这![]() 天日销售量进行统计,得到频率分布直方图如图.
天日销售量进行统计,得到频率分布直方图如图.
(Ⅰ)若已知销售量低于50的天数为23,求![]() ;
;
(Ⅱ)厂家对该超市销售这种产品的日返利方案为:每天固定返利45元,另外每销售一件产品,返利3元;频率估计为概率.依此方案,估计日返利额的平均值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com