
【题目】在如图所示的圆锥中,OP是圆锥的高,AB是底面圆的直径,点C是弧AB的中点,E是线段AC的中点,D是线段PB的中点,且PO=2,OB=1. 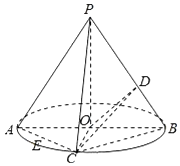
(1)试在PB上确定一点F,使得EF∥面COD,并说明理由;
(2)求点A到面COD的距离.
【答案】
(1)解:连接BE,设BE∩OC=G,由题意G为△ABC的重心,∴ ![]() =2,
=2,
连接DG,
∵EF∥平面COD,EF平面BEF,平面BEF∩平面COD=DG,
∴EF∥DG,
∴ ![]() =
= ![]() =2,
=2,
又BD=DP,∴DF=PF= ![]() PB.
PB.
∴点F是PB上靠近点P的四等分点.
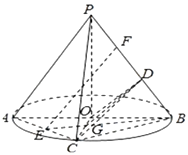
(2)解:由PO⊥平面ABC,OC平面ABC,
∴OC⊥PO,又点C是弧AB的中点,OC⊥AB,∴OC⊥平面POB.
OD平面POB,∴OC⊥OD.
S△COD= ![]() OCOD=
OCOD= ![]() =
= ![]() .
.
∵VA﹣OCD=VD﹣AOC,∴ ![]() S△CODd=
S△CODd= ![]()
![]() PO,
PO,
∴ ![]() d=
d= ![]() ,
,
∴点A到面COD的距离 ![]() .
.
【解析】(1)连接BE,设BE∩OC=G,由题意G为△ABC的重心,可得 ![]() =2,连接DG,利用EF∥平面COD,可得EF∥DG,进而得出F点的位置.(2)由PO⊥平面ABC,可得OC⊥PO,利用线面面面垂直的判定与性质定理可得OC⊥平面POB.OC⊥OD.利用VA﹣OCD=VD﹣AOC , 即可得出.
=2,连接DG,利用EF∥平面COD,可得EF∥DG,进而得出F点的位置.(2)由PO⊥平面ABC,可得OC⊥PO,利用线面面面垂直的判定与性质定理可得OC⊥平面POB.OC⊥OD.利用VA﹣OCD=VD﹣AOC , 即可得出.


科目:高中数学 来源: 题型:
【题目】设圆![]() 满足:(1)截
满足:(1)截![]() 轴所得弦长为2;(2)被
轴所得弦长为2;(2)被![]() 轴分成两段圆弧,其弧长的比为
轴分成两段圆弧,其弧长的比为![]() .在满足条件(1)、(2)的所有圆中,圆心到直线
.在满足条件(1)、(2)的所有圆中,圆心到直线![]() 的距离最小的圆的方程为__________.
的距离最小的圆的方程为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解某地区高三学生的身体发育情况,抽查了该地区100名年龄为17.5岁﹣18岁的男生体重(kg),得到频率分布直方图如图.根据图可得这100名学生中体重在〔56.5,64.5〕的学生人数是( ) 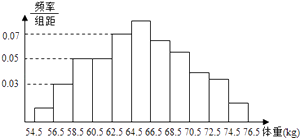
A.20
B.30
C.40
D.50
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】进行随机抽样时,甲学生认为:“每次抽取一个个体时,任一个个体a被抽到的概率”与“在整个抽样过程中个体a被抽到的概率”是一回事,而学生乙则认为两者不是一回事.你认为甲、乙两学生中哪个对?请列举具体例子加以说明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆![]() 经过点
经过点![]() ,离心率
,离心率![]() ,直线
,直线![]() 的方程为
的方程为![]() .
.
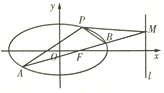
![]() 求椭圆
求椭圆![]() 的方程;
的方程;
![]()
![]() 是经过右焦点
是经过右焦点![]() 的任一弦(不经过点
的任一弦(不经过点![]() ),设直线
),设直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,记
,记![]() ,
, ![]() ,
, ![]() 的斜率为
的斜率为![]() ,
, ![]() ,
, ![]() .问:是否存在常数
.问:是否存在常数![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若a,b是函数f(x)=x2﹣px+q(p>0,q>0)的两个不同的零点,且a,b,﹣2这三个数可适当排序后成等差数列,也可适当排序后成等比数列,则p+q的值等于 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD﹣A1B1C1D1中,M,N,P分别是B1B,B1C1 , CD的中点,则MN与D1P所成角的余弦值为( ) 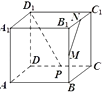
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某食品厂需要定期购买食品配料,该厂每天需要食品配料200千克,配料的价格为1.8元/千克,每次购买配料需支付运费236元,每次购买来的配料还需支付保管费用,其标准如下:7天以内(含7天),无论重量多少,均按10元/天支付;超出7天以外的天数,根据实际剩余配料的重量,以每天0.03元/千克支付.
(1)当9天购买一次配料时,求该厂用于配料的保管费用![]() 是多少元?
是多少元?
(2)设该厂![]() 天购买一次配料,求该厂在这
天购买一次配料,求该厂在这![]() 天中用于配料的总费用
天中用于配料的总费用![]() (元)关于
(元)关于![]() 的函数关系式,并求该厂多少天购买一次配料才能使平均每天支付的费用最少?
的函数关系式,并求该厂多少天购买一次配料才能使平均每天支付的费用最少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com