
【题目】若0<a<b,且a+b=1,则下列各式中最大的是( )
A.﹣1
B.log2a+log2b+1
C.log2b
D.log2(a3+a2b+ab2+b3)
【答案】C
【解析】解答:∵0<a<b,且a+b=1 ∴b ![]()
∴log2b> ![]() =﹣1
=﹣1
∵0<a<b,且a+b=1
∴a ![]()
∴log2a<﹣1
∴log2a+log2b+1<log2b
∵0<a<b,且a+b=1
∴a3+a2b+ab2+b3=a2+b2∴b﹣(a2+b2)=b(a+b)﹣a2+b2=ab﹣a2=a(b﹣a)>0
∴log2b>log2(a3+a2b+ab2+b3)
故选C
分析:本题将﹣1变为 ![]() ,根据0<a<b,且a+b=1知b
,根据0<a<b,且a+b=1知b ![]() ,a
,a ![]() 故log2b>﹣1,log2a<﹣1,故log2a+log2b+1<log2b,故只需要比较b与a3+a2b+ab2+b3的大小,根据0<a<b,且a+b=1,知a3+a2b+ab2+b3=a2+b2 , 而b=b(a+b),0<a<b即得b>a2+b2即可.
故log2b>﹣1,log2a<﹣1,故log2a+log2b+1<log2b,故只需要比较b与a3+a2b+ab2+b3的大小,根据0<a<b,且a+b=1,知a3+a2b+ab2+b3=a2+b2 , 而b=b(a+b),0<a<b即得b>a2+b2即可.
【考点精析】根据题目的已知条件,利用基本不等式的相关知识可以得到问题的答案,需要掌握基本不等式:![]()
![]() ,(当且仅当
,(当且仅当![]() 时取到等号);变形公式:
时取到等号);变形公式:![]()
![]() .
.


科目:高中数学 来源: 题型:
【题目】在“新零售”模式的背景下,某大型零售公司咪推广线下分店,计划在![]() 市的
市的![]() 区开设分店,为了确定在该区开设分店的个数,该公司对该市已开设分店听其他区的数据作了初步处理后得到下列表格.记
区开设分店,为了确定在该区开设分店的个数,该公司对该市已开设分店听其他区的数据作了初步处理后得到下列表格.记![]() 表示在各区开设分店的个数,
表示在各区开设分店的个数, ![]() 表示这个
表示这个![]() 个分店的年收入之和.
个分店的年收入之和.
| 2 | 3 | 4 | 5 | 6 |
| 2.5 | 3 | 4 | 4.5 | 6 |
(1)该公司已经过初步判断,可用线性回归模型拟合![]() 与
与![]() 的关系,求
的关系,求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)假设该公司在![]() 区获得的总年利润
区获得的总年利润![]() (单位:百万元)与
(单位:百万元)与![]() 之间的关系为
之间的关系为![]() ,请结合(1)中的线性回归方程,估算该公司应在
,请结合(1)中的线性回归方程,估算该公司应在![]() 区开设多少个分店时,才能使
区开设多少个分店时,才能使![]() 区平均每个店的年利润最大?
区平均每个店的年利润最大?
(参考公式: ![]() ,其中
,其中 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,抛物线![]() 的焦点为
的焦点为![]() .
.
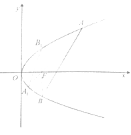
(1)求抛物线![]() 的标准方程;
的标准方程;
(2)过![]() 的两条直线分别与抛物线
的两条直线分别与抛物线![]() 交于点
交于点![]() ,
,![]() 与
与![]() ,
,![]() (点
(点![]() ,
,![]() 在
在![]() 轴的上方).
轴的上方).
①若![]() ,求直线
,求直线![]() 的斜率;
的斜率;
②设直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,若
,若![]() ,求证:直线
,求证:直线![]() 过定点.
过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列:2,0,2,0,2,0,….前六项不适合下列哪个通项公式 ( )
A.![]() =1+(―1)n+1
=1+(―1)n+1
B.![]() =2|sin
=2|sin ![]() |
|
C.![]() =1-(―1)n
=1-(―1)n
D.![]() =2sin
=2sin ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有以下4个命题:
①若 ![]() ,则a﹣c>b﹣d; ②若a≠0,b≠0,则
,则a﹣c>b﹣d; ②若a≠0,b≠0,则 ![]() ;③两条直线平行的充要条件是它们的斜率相等; ④过点(x0 , y0)与圆x2+y2=r2相切的直线方程是x0x+y0y=r2 .
;③两条直线平行的充要条件是它们的斜率相等; ④过点(x0 , y0)与圆x2+y2=r2相切的直线方程是x0x+y0y=r2 .
其中错误命题的序号是 . (把你认为错误的命题序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且过点B(0,1).
,且过点B(0,1).

(Ⅰ)求椭圆的方程;
(Ⅱ)若点A是椭圆的右顶点,点![]() 在以AB为直径的圆上,延长PB交椭圆E于点Q,求
在以AB为直径的圆上,延长PB交椭圆E于点Q,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点B与点A(﹣1,1)关于原点O对称,P是动点,且直线AP与BP的斜率之积等于﹣ ![]() .
.
(1)求动点P的轨迹方程;
(2)设直线AP和BP分别与直线x=3交于点M,N,问:是否存在点P使得△PAB与△PMN的面积相等?若存在,求出点P的坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com