
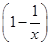 ,1<x<2.(2)当薄板长为
,1<x<2.(2)当薄板长为 m,宽为(2-
m,宽为(2- )m时,节能效果最好.(3)当薄板长为
)m时,节能效果最好.(3)当薄板长为 m,宽为(2-
m,宽为(2- )m时,制冷效果最好.
)m时,制冷效果最好.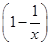 ,1<x<2.
,1<x<2.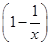 (2-x)=3-
(2-x)=3- ≤3-2
≤3-2 ,
, ∈(1,2)时,S1取得最大值.
∈(1,2)时,S1取得最大值. m,宽为(2-
m,宽为(2- )m时,节能效果最好.
)m时,节能效果最好.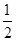 x(2-x)+
x(2-x)+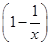 (2-x)=3-
(2-x)=3-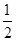
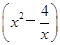 ,1<x<2.
,1<x<2. =0?x=
=0?x= .
. )上递增,在(
)上递增,在( ,2)上递减.所以当x=
,2)上递减.所以当x= 时,S2取得最大值.
时,S2取得最大值. m,宽为(2-
m,宽为(2- )m时,制冷效果最好
)m时,制冷效果最好

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:不详 题型:单选题
 ,若存在区间
,若存在区间 ,使得
,使得 ,则称函数
,则称函数 为“可等域函数”,区间
为“可等域函数”,区间 为函数
为函数 的一个“可等域区间”.给出下列4个函数:
的一个“可等域区间”.给出下列4个函数: ;②
;② ; ③
; ③ ; ④
; ④ .
.| A.①②③ | B.②③ | C.①③ | D.②③④ |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 若有一个正实根,一个负实根,则
若有一个正实根,一个负实根,则 ;
; 是偶函数,但不是奇函数;
是偶函数,但不是奇函数; 的值域是
的值域是 ,则函数
,则函数 的值域为
的值域为 ;
; 和直线
和直线 的公共点个数是
的公共点个数是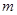 ,则
,则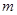 的值不可能是
的值不可能是 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
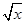 +2)=x+4
+2)=x+4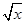 ,求f(x);
,求f(x);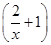 =lgx,求f(x);
=lgx,求f(x);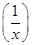 =2x,x∈R且x≠0,求f(x);
=2x,x∈R且x≠0,求f(x);查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 )x万元,假设所有桥墩都视为点且不考虑其他因素,记工程总费用为y万元.
)x万元,假设所有桥墩都视为点且不考虑其他因素,记工程总费用为y万元.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题

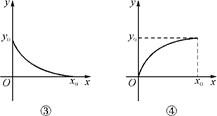
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com