
【题目】已知曲线![]()
(1)求曲线在点![]() 处的切线方程;
处的切线方程;
(2)过原点作曲线的切线![]() ,求切线方程.
,求切线方程.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)先求出函数的导函数,再求出函数在x=0处的导数即斜率,易求切线方程.
(2)设切点为(x0,y0),则直线l的斜率为f'(x0)=3x02-8,从而求得直线l的方程,由条件直线1过原点可求解切点坐标,进而可得直线1的方程.
试题解析:
(1)∵f′(x)=(x38x+2)′=3x28,
∴在点x=0处的切线的斜率k=f′(0)=8,且f(0)=2,
∴切线的方程为y=8x+2.
(2)设切点为(x0,y0),则直线l的斜率为f′(x0)=3x208,
∴直线l的方程为y=(3x208)(xx0)+x308x0+2.
又∵直线l过点(0,0),∴0=(3x208)(x0)+x308x0+2,
整理,得x30=1,∴x0=1,直线l的斜率k=3×(1)28=5,
∴直线l的方程为y=5x.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】为了调查某生产线上质量监督员甲对产品质量好坏有无影响,现统计数据如下:质量监督员甲在生产现场时,990件产品中合格品有982件,次品有8件;甲不在生产现场时,510件产品中合格品有493件,次品有17件,试分别用列联表、独立性检验的方法分析监督员甲是否在生产现场对产品质量好坏有无影响?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程.
已知曲线![]() 在直角坐标系
在直角坐标系![]() 下的参数方程为
下的参数方程为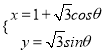 (
(![]() 为参数).以
为参数).以![]() 为极点,
为极点, ![]() 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)直线![]() 的极坐标方程是
的极坐标方程是![]() ,射线
,射线![]() 与曲线
与曲线![]() 交于
交于![]() 点,与直线
点,与直线![]() 交于
交于![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂生产![]() 和
和![]() 两种产品,按计划每天生产
两种产品,按计划每天生产![]() 各不得少于10吨,已知生产
各不得少于10吨,已知生产![]() 产品
产品![]() 吨需要用煤9吨,电4度,劳动力3个(按工作日计算).生产
吨需要用煤9吨,电4度,劳动力3个(按工作日计算).生产![]() 产品1吨需要用煤4吨,电5度,劳动力10个,如果
产品1吨需要用煤4吨,电5度,劳动力10个,如果![]() 产品每吨价值7万元,
产品每吨价值7万元, ![]() 产品每吨价值12万元,而且每天用煤不超过300吨,用电不超过200度,劳动力最多只有300个,每天应安排生产
产品每吨价值12万元,而且每天用煤不超过300吨,用电不超过200度,劳动力最多只有300个,每天应安排生产![]() 两种产品各多少才是合理的?
两种产品各多少才是合理的?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的通项公式是
的通项公式是![]() .
.
(1)判断![]() 是否是数列
是否是数列![]() 中的项;
中的项;
(2)试判断数列![]() 中的各项是否都在区间
中的各项是否都在区间![]() 内;
内;
(3)试判断在区间![]() 内是否有无穷数列
内是否有无穷数列![]() 中的项?若有,是第几项?若没有,请说明理由.
中的项?若有,是第几项?若没有,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业常年生产一种出口产品,根据预测可知,进入21世纪以来,该产品的产量平稳增长.记2009年为第1年,且前4年中,第x年与年产量f(x) 万件之间的关系如下表所示:
x | 1 | 2 | 3 | 4 |
f(x) | 4.00 | 5.58 | 7.00 | 8.44 |
若f(x)近似符合以下三种函数模型之一:f(x)=ax+b,f(x)=2x+a,f(x)=log![]() x+a.
x+a.
(1)找出你认为最适合的函数模型,并说明理由,然后选取其中你认为最适合的数据求出相应的解析式;
(2)因遭受某国对该产品进行反倾销的影响,2015年的年产量比预计减少30%,试根据所建立的函数模型,确定2015年的年产量.
查看答案和解析>>
科目:高中数学 来源: 题型:
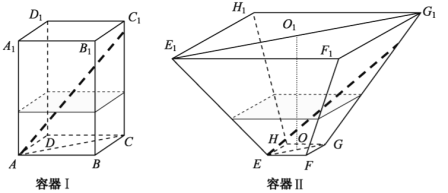
【题目】如图,水平放置的正四棱柱形玻璃容器Ⅰ和正四棱台形玻璃容器Ⅱ的高均为32cm,容器Ⅰ的底面对角线AC的长为10![]() cm,容器Ⅱ的两底面对角线
cm,容器Ⅱ的两底面对角线![]() ,
,![]() 的长分别为14cm和62cm.分别在容器Ⅰ和容器Ⅱ中注入水,水深均为12cm.现有一根玻璃棒l,其长度为40cm.(容器厚度、玻璃棒粗细均忽略不计)
的长分别为14cm和62cm.分别在容器Ⅰ和容器Ⅱ中注入水,水深均为12cm.现有一根玻璃棒l,其长度为40cm.(容器厚度、玻璃棒粗细均忽略不计)
(1)将![]() 放在容器Ⅰ中,
放在容器Ⅰ中,![]() 的一端置于点A处,另一端置于侧棱
的一端置于点A处,另一端置于侧棱![]() 上,求
上,求![]() 没入水中部分的长度;
没入水中部分的长度;
(2)将![]() 放在容器Ⅱ中,
放在容器Ⅱ中,![]() 的一端置于点E处,另一端置于侧棱
的一端置于点E处,另一端置于侧棱![]() 上,求
上,求![]() 没入水中部分的长度.
没入水中部分的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com