
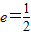 .
.
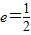 ,建立方程组,求得几何量,即可得到椭圆E的方程;
,建立方程组,求得几何量,即可得到椭圆E的方程;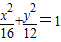 ,求得BC中点代入直线2x-y-1=0上,即可得到结论.
,求得BC中点代入直线2x-y-1=0上,即可得到结论.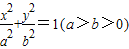
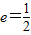
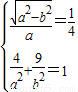
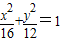 ;
;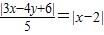 .
. 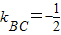
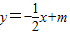 代人
代人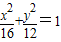 得x2-mx+m2-12=0,
得x2-mx+m2-12=0,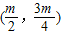


 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:高中数学 来源: 题型:
 已知椭圆E经过点A(2,3),对称轴为坐标轴,焦点F1,F2在x轴上,离心率e=
已知椭圆E经过点A(2,3),对称轴为坐标轴,焦点F1,F2在x轴上,离心率e=| 1 | 2 |
查看答案和解析>>
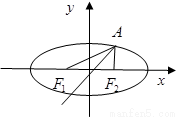
科目:高中数学 来源:2013届吉林省高二期中考试文科数学试卷(解析版) 题型:解答题
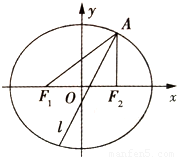
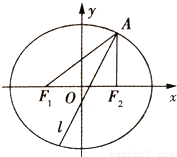
如图,已知椭圆E经过点A(2,3),对称轴为坐标轴,焦点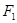 、
、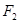 在x轴上,离心率
在x轴上,离心率
(1)求椭圆E的方程;
(2)求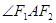 的角平分线所在直线
的角平分线所在直线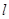 的方程.
的方程.
查看答案和解析>>
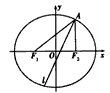
科目:高中数学 来源:安徽省高考真题 题型:解答题
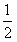 ,
,
查看答案和解析>>
科目:高中数学 来源:2013年山东省淄博市高考数学模拟试卷1(理科)(解析版) 题型:解答题
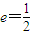 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com