
【题目】已知函数![]() ,其图象与
,其图象与![]() 轴交于不同两点
轴交于不同两点![]() ,
,![]() ,且
,且![]() .
.
(1)求实数![]() 的取值范围;
的取值范围;
(2)证明:![]() .
.
【答案】(1)![]() (2)证明见解析
(2)证明见解析
【解析】
(1)先变量分离得![]() ,再利用导数研究函数
,再利用导数研究函数![]() 的单调性和极值,即得解;(2)先利用导数证明
的单调性和极值,即得解;(2)先利用导数证明![]() ,再证明
,再证明![]() ,不等式即得证.
,不等式即得证.
(1)由![]() ,得
,得![]() .
.
令![]() ,则
,则![]() .
.
由![]() ,解得
,解得![]() ,所以
,所以![]() 在区间
在区间![]() 上单调递增;
上单调递增;
由![]() ,解得
,解得![]() ,所以
,所以![]() 在区间
在区间![]() 上单调递减;
上单调递减;
于是![]() 在
在![]() 处取得极小值,且
处取得极小值,且![]() .
.
又![]() 时,
时,![]() ,
,
由于要使![]() 的图象与直线
的图象与直线![]() 有两个不同的交点,
有两个不同的交点,
所以![]() .
.
(2)由(1)知![]() .
.
一方面,令![]() ,
,![]() ,
,
则![]() ,
,
又令![]() ,
,![]() ,
,
则![]() .
.
易知![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() ,
,
则![]() 在
在![]() 上单调递减,所以
上单调递减,所以![]() ,于是
,于是![]() ,
,
所以![]() 在
在![]() 上单调递增.则
上单调递增.则![]() ,即
,即![]() .
.
所以![]() .
.
又![]() 在区间
在区间![]() 上单调递增,所以
上单调递增,所以![]() ,即
,即![]() .
.
另一方面,令![]() ,则
,则![]() ,
,
易知在![]() 时,
时,![]() 取得最小值
取得最小值![]() ,所以
,所以![]() ,即
,即![]() .
.
![]() ,∴
,∴![]() .
.
∵![]() ,∴方程
,∴方程![]() 有唯一正根
有唯一正根![]() ,则
,则![]() .
.
又![]() ,
,![]() 在区间
在区间![]() 单调递增,
单调递增,
所以根据零点存在定理,得![]() 在区间
在区间![]() 有唯一零点
有唯一零点![]() .
.
所以![]() ,
,
又![]() ,②
,②
①代入②,得![]() ,解得
,解得![]() .
.
于是![]() .
.
令![]() ,
,![]() ,则
,则
![]()
又令![]() ,则
,则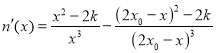 .
.
注意到![]() 为减函数,所以
为减函数,所以![]() ,
,
于是![]() ,从而
,从而![]() 为增函数,所以
为增函数,所以![]() ,
,
故![]() 为减函数,则
为减函数,则![]() ,即
,即![]() .
.
所以![]() ,
,
又![]() 在区间
在区间![]() 上单调递增,所以
上单调递增,所以![]() ,即
,即![]() .
.
综上,![]() .
.


科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在极坐标系中,已知曲线![]() ,将曲线
,将曲线![]() 上的点向左平移一个单位,然后纵坐标不变,横坐标轴伸长到原来的2倍,得到曲线
上的点向左平移一个单位,然后纵坐标不变,横坐标轴伸长到原来的2倍,得到曲线![]() ,又已知直线
,又已知直线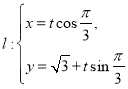 (
(![]() 是参数),且直线
是参数),且直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点.
两点.
(I)求曲线![]() 的直角坐标方程,并说明它是什么曲线;
的直角坐标方程,并说明它是什么曲线;
(II)设定点![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了让贫困地区的孩子们过一个温暖的冬天,某校阳光志愿者社团组织“这个冬天不再冷”冬衣募捐活动,共有50名志愿者参与.志愿者的工作内容有两项:①到各班做宣传,倡议同学们积极捐献冬衣;②整理、打包募捐上来的衣物.每位志愿者根据自身实际情况,只参与其中的某一项工作.相关统计数据如下表所示:

(1)如果用分层抽样的方法从参与两项工作的志愿者中抽取5人,再从这5人中选2人,那么“至少有1人是参与班级宣传的志愿者”的概率是多少?
(2)若参与班级宣传的志愿者中有12名男生,8名女生,从中选出2名志愿者,用![]() 表示所选志愿者中的女生人数,写出随机变量
表示所选志愿者中的女生人数,写出随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十九大提出对农村要坚持精准扶贫,至2020年底全面脱贫.现有扶贫工作组到某山区贫困村实施脱贫工作.经摸底排查,该村现有贫闲农户100家,他们均从事水果种植,2017年底该村平均每户年纯收入为1万元.扶贫工作组一方面请有关专家对果树进行品种改良,提高产量;另一方面,抽出部分农户从事水果包装、销售工作,其人数必须小于种植的人数.从2018年初开始,该村抽出![]() 户(
户(![]() )从事水果包装、销售.经测算,剩下从事水果种植农户的年纯收入每户平均比上一年提高
)从事水果包装、销售.经测算,剩下从事水果种植农户的年纯收入每户平均比上一年提高![]() ,而从事包装销售农户的年纯收入每户平均为
,而从事包装销售农户的年纯收入每户平均为![]() 万元(参考数据:
万元(参考数据:![]() ).
).
(1)至2020年底,为使从事水果种植农户能实现脱贫(每户年均纯收入不低于1万5千元),则应至少抽出多少户从事包装、销售工作?
(2)至2018年底,该村每户年均纯收人能否达到1.355万元?若能,请求出从事包装、销售的户数;若不能,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 和
和![]() 都是等差数列,
都是等差数列,![]() .数列
.数列![]() 满足
满足![]() .
.
(1)求![]() 的通项公式;
的通项公式;
(2)证明:![]() 是等比数列;
是等比数列;
(3)是否存在首项为1,公比为q的等比数列![]() ,使得对任意
,使得对任意![]() ,都有
,都有![]() 成立?若存在,求出q的取值范围;若不存在,请说明理由.
成立?若存在,求出q的取值范围;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com