
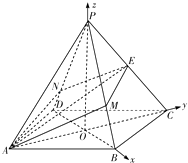
【题目】如图,在正四棱锥P﹣ABCD中,AB=2,PA= ![]() ,E是棱PC的中点,过AE作平面分别与棱PB、PD交于M、N两点.
,E是棱PC的中点,过AE作平面分别与棱PB、PD交于M、N两点. 
(1)若PM= ![]() PB,PN=λPD,求λ的值;
PB,PN=λPD,求λ的值;
(2)求直线PA与平面AMEN所成角的正弦值的取值范围.
【答案】
(1)解:连接AC、BD交于点O,以O为坐标原点建立如图所示的空间直角坐标系,则A(0,﹣ ![]() ,0),B (
,0),B ( ![]() ,0,0),C(0,
,0,0),C(0, ![]() ,0),D(﹣
,0),D(﹣ ![]() ,0,0),P(0,0,2),E(0,
,0,0),P(0,0,2),E(0, ![]() ,1)
,1)
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
![]() ,
,
∵AN,AE,AM共面,∴ ![]()
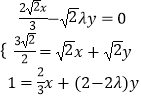
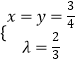
(2)解:根据正四棱锥P﹣ABCD的对称性可知,当PM=PN时,P到面AMEN的距离最大,此时直线PA与平面AMEN所角最大,
,P到面AMEN的距离最小,此时直线PA与平面AMEN所角最小.
①由(Ⅰ)知当PM=PN时,λ= ![]() ,
, ![]() ,
,
设面AMEN的法向量为 ![]() ,
,
由 ![]() ,
, ![]() 取
取 ![]()
设直线PA与平面AMEN所成角为θ,sinθ=|cos< ![]() >|=
>|= ![]() ,
,
②当M在B时,因为AB∥面PDC,所以过AB,AE的面与面PDC的交线NE∥AB
设 ![]() 是面ABEN的法向量,
是面ABEN的法向量,
由 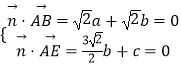 ,可取
,可取 ![]()
sinθ=|cos< ![]() >|=
>|= ![]() .
.
直线PA与平面AMEN所成角的正弦值的取值范围为[ ![]() ,
, ![]() ]
]
【解析】(1)连接AC、BD交于点O,以O为坐标原点建立如图所示的空间直角坐标系,则A(0,﹣ ![]() ,0),B (
,0),B ( ![]() ,0,0),C(0,
,0,0),C(0, ![]() ,0),D(﹣
,0),D(﹣ ![]() ,0,0),P(0,0,2),E(0,
,0,0),P(0,0,2),E(0, ![]() ,1)由AN,AE,AM共面,
,1)由AN,AE,AM共面, ![]()
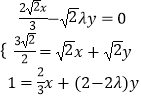
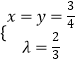 .(2)根据正四棱锥P﹣ABCD的对称性可知,当PM=PN时,P到面AMEN的距离最大,此时直线PA与平面AMEN所角最大,P到面AMEN的距离最小,此时直线PA与平面AMEN所角最小.利用向量分别求出求解直线PA与平面AMEN所成角的正弦值.
.(2)根据正四棱锥P﹣ABCD的对称性可知,当PM=PN时,P到面AMEN的距离最大,此时直线PA与平面AMEN所角最大,P到面AMEN的距离最小,此时直线PA与平面AMEN所角最小.利用向量分别求出求解直线PA与平面AMEN所成角的正弦值.
【考点精析】本题主要考查了空间角的异面直线所成的角的相关知识点,需要掌握已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则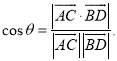 才能正确解答此题.
才能正确解答此题.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:高中数学 来源: 题型:
【题目】某幼儿园为训练孩子的数字运算能力,在一个盒子里装有标号为1,2,3,4,5的卡片各两张,让孩子从盒子里任取3张卡片,按卡片上的最大数字的9倍计分,每张卡片被取出的可能性都相等,用X表示取出的3张卡片上的最大数字
(1)求取出的3张卡片上的数字互不相同的概率;
(2)求随机变量X的分布列及数学期望;
(3)若孩子取出的卡片的计分超过30分,就得到奖励,求孩子得到奖励的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x+2a|+|x﹣1|,a∈R.
(1)当a=1时,解不等式f(x)≤5;
(2)若f(x)≥2对于x∈R恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,有两个独立的转盘(![]() )、(
)、(![]() ).两个图中三个扇形区域的圆心角分别为
).两个图中三个扇形区域的圆心角分别为![]() 、
、![]() 、
、![]() .用这两个转盘进行玩游戏,规则是:依次随机转动两个转盘再随机停下(指针固定不会动,当指针恰好落在分界线时,则这次结果无效,重新开始),记转盘(
.用这两个转盘进行玩游戏,规则是:依次随机转动两个转盘再随机停下(指针固定不会动,当指针恰好落在分界线时,则这次结果无效,重新开始),记转盘(![]() )指针所对的数为
)指针所对的数为![]() ,转盘(
,转盘(![]() )指针所对的数为
)指针所对的数为![]() ,(
,(![]() 、
、![]() ),求下列概率:
),求下列概率:

(1)![]() ;
;
(2)![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数![]() 的图象向右平移
的图象向右平移![]() 个单位长度,所得图像对应的函数( )
个单位长度,所得图像对应的函数( )
A. 在区间![]() 上单调递减 B. 在区间
上单调递减 B. 在区间![]() 上单调递增
上单调递增
C. 在区间![]() 上单调递减 D. 在区间
上单调递减 D. 在区间![]() 上单调递增
上单调递增
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C所对的边分别为a,b,c.向量 ![]() =(a,
=(a, ![]() b)与
b)与 ![]() =(cosA,sinB)平行.
=(cosA,sinB)平行.
(Ⅰ)求A;
(Ⅱ)若a= ![]() ,b=2,求△ABC的面积.
,b=2,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图象与
的图象与![]() 轴的交点中相邻两个交点的距离是
轴的交点中相邻两个交点的距离是![]() ,当
,当![]() 时
时![]() 取得最小值
取得最小值![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)求函数![]() 在区间
在区间![]() 的最大值和最小值;
的最大值和最小值;
(3)若函数![]() 的零点为
的零点为![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角梯形![]() 中,
中, ![]() ,
, ![]() 为线段
为线段![]() (含端点)上一个动点,设
(含端点)上一个动点,设![]() 对于函数
对于函数![]() ,给出以下三个结论:
,给出以下三个结论:
①当![]() 时,函数
时,函数![]() 的值域为
的值域为![]() ;
;
②对于任意的![]() ,均有
,均有![]() ;
;
③对于任意的![]() ,函数
,函数![]() 的最大值均为4.
的最大值均为4.
其中所有正确的结论序号为__________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com