
【题目】在正方体![]() 中,点
中,点![]() 、
、![]() 分别是棱
分别是棱![]() 和
和![]() 的中点,给出下列结论:
的中点,给出下列结论:
①直线![]() 与
与![]() 所成角为
所成角为![]() ;②正方体的所有棱中与直线
;②正方体的所有棱中与直线![]() 异面的有
异面的有![]() 条;③直线
条;③直线![]() 平面
平面![]() ;④平面
;④平面![]() 平面
平面![]() .其中正确的是( )
.其中正确的是( )
A.①②B.②③C.②④D.①④
【答案】D
【解析】
作出图形,推导出![]() ,求得
,求得![]() ,可判断命题①的正误;利用异面直线的概念可判断命题②的正误;利用线面平行的判定定理可判断命题③的正误;利用面面垂直的判定定理可判断命题④的正误.综合可得出结论.
,可判断命题①的正误;利用异面直线的概念可判断命题②的正误;利用线面平行的判定定理可判断命题③的正误;利用面面垂直的判定定理可判断命题④的正误.综合可得出结论.
对于命题①,如下图所示:
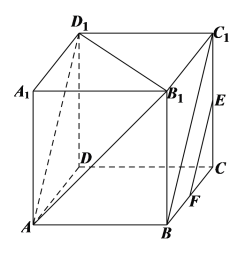
连接![]() 、
、![]() 、
、![]() ,
,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,则
的中点,则![]() ,
,
在正方体![]() ,
,![]() 且
且![]() ,
,![]() 且
且![]() ,
,
![]() 且
且![]() ,
,![]() 四边形
四边形![]() 为平行四边形,
为平行四边形,![]() ,
,![]() ,
,
所以,异面直线![]() 与
与![]() 所成角为
所成角为![]() ,
,
易知![]() 是等边三角形,则
是等边三角形,则![]() ,所以,直线
,所以,直线![]() 与
与![]() 所成角为
所成角为![]() ,
,
命题①正确;
对于命题②,在正方体![]() 中,与
中,与![]() 异面的棱有
异面的棱有![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,共
,共![]() 条,命题②错误;
条,命题②错误;
对于命题③,在正方体![]() 中,
中,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,![]() ,
,
![]() 四边形
四边形![]() 为正方形,则
为正方形,则![]() ,
,
![]() ,
,![]() 平面
平面![]() ,
,
若![]() 平面
平面![]() ,则平面
,则平面![]() 平面
平面![]() ,矛盾.
,矛盾.
命题③错误;
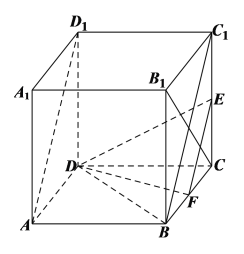
对于命题④,如下图所示:

![]() 四边形
四边形![]() 为正方形,
为正方形,![]() ,
,
在正方体![]() 中,
中,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,
![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() 平面
平面![]() ,命题④正确.
,命题④正确.
故选:D.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,如图,已知椭圆E:
中,如图,已知椭圆E:![]() 的左、右顶点分别为
的左、右顶点分别为![]() 、
、![]() ,上、下顶点分别为
,上、下顶点分别为![]() 、
、![]() .设直线
.设直线![]() 倾斜角的余弦值为
倾斜角的余弦值为![]() ,圆
,圆![]() 与以线段
与以线段![]() 为直径的圆关于直线
为直径的圆关于直线![]() 对称.
对称.

(1)求椭圆E的离心率;
(2)判断直线![]() 与圆
与圆![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(3)若圆![]() 的面积为
的面积为![]() ,求圆
,求圆![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某手机生产企业为了对研发的一批最新款手机进行合理定价,将该款手机按事先拟定的价格进行试销,得到单价![]() (单位:千元)与销量
(单位:千元)与销量![]() (单位:百件)的关系如下表所示:
(单位:百件)的关系如下表所示:
单价 | 1 | 1.5 | 2 | 2.5 | 3 |
销量 | 10 | 8 | 7 | 6 |
|
已知![]() .
.
(Ⅰ)若变量![]() ,
,![]() 具有线性相关关系,求产品销量
具有线性相关关系,求产品销量![]() (百件)关于试销单价
(百件)关于试销单价![]() (千元)的线性回归方程
(千元)的线性回归方程![]() ;
;
(Ⅱ)用(Ⅰ)中所求的线性回归方程得到与![]() 对应的产品销量的估计值
对应的产品销量的估计值![]() ,当销售数据
,当销售数据![]() 对应的残差满足
对应的残差满足![]() 时,则称
时,则称![]() 为一个“好数据”,现从5个销售数据中任取3个,求其中“好数据”的个数
为一个“好数据”,现从5个销售数据中任取3个,求其中“好数据”的个数![]() 的分布列和数学期望.
的分布列和数学期望.
参考公式: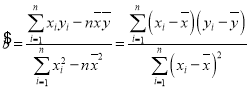 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知离心率为![]() 的椭圆
的椭圆![]() ,
,![]() 经过抛物线
经过抛物线![]() 的焦点
的焦点![]() ,斜率为1的直线
,斜率为1的直线![]() 经过
经过![]() 且与椭圆交于
且与椭圆交于![]() 两点.
两点.
(1)求![]() 面积;
面积;
(2)动直线![]() 与椭圆有且仅有一个交点,且与直线
与椭圆有且仅有一个交点,且与直线![]() ,
,![]() 分别交于
分别交于![]() 两点,且
两点,且![]() 为椭圆的右焦点,证明
为椭圆的右焦点,证明![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等边![]() 的边长为
的边长为![]() ,点
,点![]() ,
,![]() 分别是
分别是![]() ,
,![]() 上的点,且满足
上的点,且满足![]() (如图(1)),将
(如图(1)),将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使二面角
的位置,使二面角![]() 成直二面角,连接
成直二面角,连接![]() ,
,![]() (如图(2)).
(如图(2)).
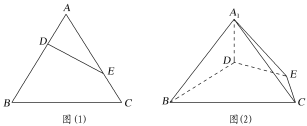
(1)求证:![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使直线
,使直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某高中女学生中选取10名学生,根据其身高![]() 、体重
、体重![]() 数据,得到体重关于身高的回归方程
数据,得到体重关于身高的回归方程![]() ,用来刻画回归效果的相关指数
,用来刻画回归效果的相关指数![]() ,则下列说法正确的是( )
,则下列说法正确的是( )
A.这些女学生的体重和身高具有非线性相关关系
B.这些女学生的体重差异有60%是由身高引起的
C.身高为![]() 的女学生的体重一定为
的女学生的体重一定为![]()
D.这些女学生的身高每增加![]() ,其体重约增加
,其体重约增加![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线L的参数方程为:![]() ,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为
,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为![]() .
.
(Ⅰ)求曲线C的参数方程;
(Ⅱ)当![]() 时,求直线l与曲线C交点的极坐标.
时,求直线l与曲线C交点的极坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校需要从甲、乙两名学生中选一人参加数学竞赛,抽取了近期两人![]() 次数学考试的成绩,统计结果如下表:
次数学考试的成绩,统计结果如下表:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
甲的成绩(分) |
|
|
|
|
|
乙的成绩(分) |
|
|
|
|
|
(1)若从甲、乙两人中选出一人参加数学竞赛,你认为选谁合适?请说明理由.
(2)若数学竞赛分初赛和复赛,在初赛中有两种答题方案:
方案一:每人从![]() 道备选题中任意抽出
道备选题中任意抽出![]() 道,若答对,则可参加复赛,否则被淘汰.
道,若答对,则可参加复赛,否则被淘汰.
方案二:每人从![]() 道备选题中任意抽出
道备选题中任意抽出![]() 道,若至少答对其中
道,若至少答对其中![]() 道,则可参加复赛,否则被润汰.
道,则可参加复赛,否则被润汰.
已知学生甲、乙都只会![]() 道备选题中的
道备选题中的![]() 道,那么你推荐的选手选择哪种答题方条进人复赛的可能性更大?并说明理由.
道,那么你推荐的选手选择哪种答题方条进人复赛的可能性更大?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com