
【题目】如图,圆台![]() 的轴截面为等腰梯形
的轴截面为等腰梯形![]() ,
,![]() 圆台
圆台![]() 的侧面积为
的侧面积为![]() .若点
.若点![]() 分别为圆
分别为圆![]() 上的动点,且点
上的动点,且点![]() 在平面
在平面![]() 的同侧.
的同侧.

(1)求证:![]() ;
;
(2)若![]() ,则当三棱锥
,则当三棱锥![]() 的体积取最大值时,求多面体
的体积取最大值时,求多面体![]() 的体积.
的体积.
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:高中数学 来源: 题型:
【题目】某地为改善旅游环境进行景点改造.如图,将两条平行观光道l1和l2通过一段抛物线形状的栈道AB连通(道路不计宽度),l1和l2所在直线的距离为0.5(百米),对岸堤岸线l3平行于观光道且与l2相距1.5(百米)(其中A为抛物线的顶点,抛物线的对称轴垂直于l3,且交l3于M),在堤岸线l3上的E,F两处建造建筑物,其中E,F到M的距离为1(百米),且F恰在B的正对岸(即BF⊥l3).
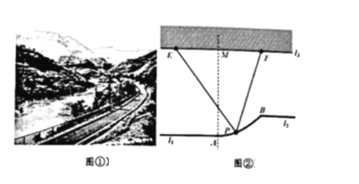
(1)在图②中建立适当的平面直角坐标系,并求栈道AB的方程;
(2)游客(视为点P)在栈道AB的何处时,观测EF的视角(∠EPF)最大?请在(1)的坐标系中,写出观测点P的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年国庆节假期期间,某商场为掌握假期期间顾客购买商品人次,统计了10月1日7:00﹣23:00这一时间段内顾客购买商品人次,统计发现这一时间段内顾客购买商品共5000人次顾客购买商品时刻的的频率分布直方图如下图所示,其中时间段7:0011:00,11:0015:00,15:00~19:00,19:00~23:00,依次记作[7,11),[11,15),[15,19),[19,23].
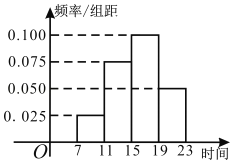
(1)求该天顾客购买商品时刻的中位数t与平均值![]() (同一组中的数据用该组区间的中点值代表);
(同一组中的数据用该组区间的中点值代表);
(2)由频率分布直方图可以近似认为国庆节假期期间该商场顾客购买商品时刻服从正态分布N(μ,δ2),其中μ近似为![]() ,δ=3.6,估计2019年国庆节假期期间(10月1日﹣10月7日)该商场顾客在12:12﹣19:24之间购买商品的总人次(结果保留整数);
,δ=3.6,估计2019年国庆节假期期间(10月1日﹣10月7日)该商场顾客在12:12﹣19:24之间购买商品的总人次(结果保留整数);
(3)为活跃节日气氛,该商场根据题中的4个时间段分组,采用分层抽样的方法从这5000个样本中随机抽取10个样本(假设这10个样本为10个不同顾客)作为幸运客户,再从这10个幸运客户中随机抽取4人每人奖励500元购物券,其他幸运客户每人奖励200元购物券,记获得500元购物券的4人中在15:00﹣19:00之间购买商品的人数为X,求X的分布列与数学期望;
参考数据:若T~N(μ,σ2),则①P(μ﹣σ<T≤μ+σ)=0.6827;②P(μ﹣2σ<T≤μ+2σ)=0.9545;③P(μ﹣3σ<T≤μ+3σ)=0.9973.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】曲线![]() 的参数方程为
的参数方程为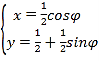 (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() ,
,![]() 的交点分别为
的交点分别为![]() 、
、![]() (
(![]() 、
、![]() 异于原点),当斜率
异于原点),当斜率![]() 时,求
时,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】改革开放以来,中国快递行业持续快速发展,快递业务量从上世纪![]() 年代的
年代的![]() 万件提升到2018年的
万件提升到2018年的![]() 亿件,快递行业的发展也给我们的生活带来了很大便利.已知某市某快递点的收费标准为:首重(重量小于等于
亿件,快递行业的发展也给我们的生活带来了很大便利.已知某市某快递点的收费标准为:首重(重量小于等于![]() )收费
)收费![]() 元,续重
元,续重![]() 元
元![]() (不足
(不足![]() 按
按![]() 算). (如:一个包裹重量为
算). (如:一个包裹重量为![]() 则需支付首付
则需支付首付![]() 元,续重
元,续重![]() 元,一共
元,一共![]() 元快递费用)
元快递费用)
(1)若你有三件礼物![]() 重量分别为
重量分别为![]() ,要将三个礼物分成两个包裹寄出(如:
,要将三个礼物分成两个包裹寄出(如:![]() 合为一个包裹,
合为一个包裹,![]() 一个包裹),那么如何分配礼物,使得你花费的快递费最少?
一个包裹),那么如何分配礼物,使得你花费的快递费最少?
(2)对该快递点近![]() 天的每日揽包裹数(单位:件)进行统计,得到的日揽包裹数分别为
天的每日揽包裹数(单位:件)进行统计,得到的日揽包裹数分别为![]() 件,
件,![]() 件,
件,![]() 件,
件,![]() 件,
件,![]() 件,那么从这
件,那么从这![]() 天中随机抽出
天中随机抽出![]() 天,求这
天,求这![]() 天的日揽包裹数均超过
天的日揽包裹数均超过![]() 件的概率.
件的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某房地产开发商在其开发的某小区前修建了一个弓形景观湖.如图,该弓形所在的圆是以![]() 为直径的圆,且
为直径的圆,且![]() 米,景观湖边界
米,景观湖边界![]() 与
与![]() 平行且它们间的距离为
平行且它们间的距离为![]() 米.开发商计划从
米.开发商计划从![]() 点出发建一座景观桥(假定建成的景观桥的桥面与地面和水面均平行),桥面在湖面上的部分记作
点出发建一座景观桥(假定建成的景观桥的桥面与地面和水面均平行),桥面在湖面上的部分记作![]() .设
.设![]() .
.
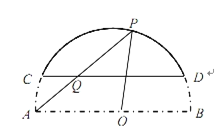
(1)用![]() 表示线段
表示线段![]() 并确定
并确定![]() 的范围;
的范围;
(2)为了使小区居民可以充分地欣赏湖景,所以要将![]() 的长度设计到最长,求
的长度设计到最长,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com