
【题目】小王、小李在两次数学考试中答对题数如下表表示:
题型 答对 题数 姓名 | 期中考试 | 期末考试 | ||||
填空题 (每题3分) | 选择题 每题3分) | 解答题 (每题8分) | 填空题 (每题3分) | 选择题 每题3分) | 解答题 (每题8分) | |
小王 | 10 | 3 | 2 | 11 | 4 | 4 |
小李 | 9 | 5 | 3 | 7 | 3 | 3 |
(1)用矩阵表示小王和小李期中考试答对题数、期末考试答对题数、每种题型的分值;
(2)用矩阵运算表示他们在两次考试中各题型答对题总数;
(3)用矩阵计算小王、小李两次考试各题型平均答对题数;
(4)用矩阵计算他们期中、期末的成绩;
(5)如果期中考试成绩占40%,期末考试成绩占60%,用矩阵求两同学的总评成绩.
科目:高中数学 来源: 题型:
【题目】王明、李东、张红三位同学在第一、第二学期消费的部分文具的数量如表所示:
姓名 | 第一学期 | 第二学期 | ||||||
笔记本 | 练习本 | 水笔 | 铅笔 | 笔记本 | 练习本 | 水笔 | 铅笔 | |
王明 | 3 | 5 | 2 | 4 | 4 | 6 | 3 | 3 |
李东 | 2 | 6 | 3 | 3 | 4 | 8 | 5 | 2 |
张红 | 4 | 7 | 4 | 2 | 5 | 10 | 6 | 4 |
若笔记本的单价为每本5元;练习本每本2元;水笔每支3元;铅笔每支1元.求三位学生在这些文具上各自花费的金额.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学为了解中学生的课外阅读时间,决定在该中学的1200名男生和800名女生中按分层抽样的方法抽取20名学生,对他们的课外阅读时间进行问卷调查。现在按课外阅读时间的情况将学生分成三类:A类(不参加课外阅读),B类(参加课外阅读,但平均每周参加课外阅读的时间不超过3小时),C类(参加课外阅读,且平均每周参加课外阅读的时间超过3小时)。调查结果如下表:
A类 | B类 | C类 | |
男生 | x | 5 | 3 |
女生 | y | 3 | 3 |
(I)求出表中x,y的值;
(II)根据表中的统计数据,完成下面的列联表,并判断是否有90%的把握认为“参加课外阅读与否”与性别有关;
男生 | 女生 | 总计 | |
不参加课外阅读 | |||
参加课外阅读 | |||
总计 |
(III)从抽出的女生中再随机抽取3人进一步了解情况,记X为抽取的这3名女生中A类人数和C类人数差的绝对值,求X的数学期望。
附:K2=![]() )
)
P(K2≥k0) | 0.10 | 0.01 | |
k0 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了了解民众对开展创建文明城市工作以来的满意度,随机调查了40名群众,并将他们随机分成A,B两组,每组20人,A组群众给第一阶段的创文工作评分,B组群众给第二阶段的创文工作评分,根据两组群众的评分绘制了如下茎叶图:
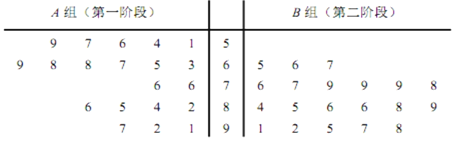
![]() 根据茎叶图比较群众对两个阶段创文工作满意度评分的平均值及集中程度
根据茎叶图比较群众对两个阶段创文工作满意度评分的平均值及集中程度![]() 不要求计算出具体值,给出结论即可
不要求计算出具体值,给出结论即可![]() ;
;
![]() 根据群众的评分将满意度从低到高分为三个等级:
根据群众的评分将满意度从低到高分为三个等级:
满意度评分 | 低于70分 | 70分到89分 | 不低于90分 |
满意度等级 | 不满意 | 满意 | 非常满意 |
![]() 假设两组群众的评价结果相互独立,由频率估计概率,求创文工作第二阶段的民众满意度等级高于第一阶段的概率;
假设两组群众的评价结果相互独立,由频率估计概率,求创文工作第二阶段的民众满意度等级高于第一阶段的概率;
![]() 从这40名群众中随机抽取2人,记X表示满意度等级为“非常满意”的群众人数,求X的分布列与数学期望.
从这40名群众中随机抽取2人,记X表示满意度等级为“非常满意”的群众人数,求X的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国全力抗击“新冠疫情”对全球做出了巨大贡献,广大中小学生在这场“战疫”中也通过各种方式作出了贡献.某校团委准备组织一次“网上战疫”的宣传活动,活动包含4项子活动.现随机抽取了5个班级中的25名同学进行关于活动方案的问卷调查,其中关于4项子活动的赞同情况统计如下:
班级代码 | A | B | C | D | E | 合计 |
4项子活动全部赞同的人数 | 3 | 4 | 8 | 3 | 2 | 20 |
4项子活动不全部赞同的人数 | 1 | 1 | 0 | 2 | 1 | 5 |
合计问卷调查人数 | 4 | 5 | 8 | 5 | 3 | 25 |
现欲针对4项子活动的活动内容作进一步采访调研,每项子活动采访1名学生.
(1)若每项子活动都从这25名同学中随机选取1人采访,求4次采访中恰有1次采访的学生对“4项子活动不全部赞同”的概率;
(2)若从A班和E班的被问卷调查者中各随机选取2人作为采访调研的对象,记选取的4人中“4项子活动全部赞同”的人数为X,求随机变量X的分布列与数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
极坐标系的极点为直角坐标系![]() 的原点,极轴为
的原点,极轴为![]() 轴的正半轴,两种坐标系中的长度单位相同,已知曲线
轴的正半轴,两种坐标系中的长度单位相同,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的直角坐标方程;
的直角坐标方程;
(2)直线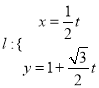 (
(![]() 为参数)与曲线
为参数)与曲线![]() 交于
交于![]() 两点,与
两点,与![]() 轴交于
轴交于![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为“中学数学联赛”选拔人才,分初赛和复赛两个阶段进行,规定:分数不小于本次考试成绩中位数的具有复赛资格,某校有900名学生参加了初赛,所有学生的成绩均在区间![]() 内,其频率分布直方图如图.
内,其频率分布直方图如图.

(1)求获得复赛资格应划定的最低分数线;
(2)从初赛得分在区间![]() 的参赛者中,利用分层抽样的方法随机抽取7人参加学校座谈交流,那么从得分在区间
的参赛者中,利用分层抽样的方法随机抽取7人参加学校座谈交流,那么从得分在区间![]() 与
与![]() 各抽取多少人?
各抽取多少人?
(3)从(2)抽取的7人中,选出4人参加全市座谈交流,设![]() 表示得分在
表示得分在![]() 中参加全市座谈交流的人数,学校打算给这4人一定的物质奖励,若该生分数在
中参加全市座谈交流的人数,学校打算给这4人一定的物质奖励,若该生分数在![]() 给予500元奖励,若该生分数在
给予500元奖励,若该生分数在![]() 给予800元奖励,用Y表示学校发的奖金数额,求Y的分布列和数学期望。
给予800元奖励,用Y表示学校发的奖金数额,求Y的分布列和数学期望。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com