
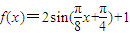 .
.
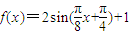 在一个周期[-2,14]上的图象.
在一个周期[-2,14]上的图象.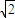 cos
cos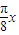 +2,令g(x)=0,可得 cos
+2,令g(x)=0,可得 cos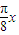 =-
=-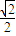 ,由此求得函数y=g(x)与x轴交点的横坐标x的值.
,由此求得函数y=g(x)与x轴交点的横坐标x的值.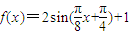 的周期等于16,列表作图如下:
的周期等于16,列表作图如下: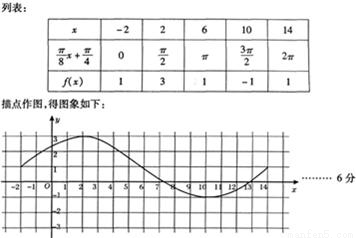
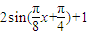 +
+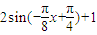
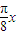 cos
cos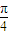 +2cos
+2cos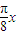 sin
sin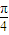 -2sin
-2sin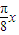 cos
cos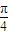 +2cos
+2cos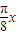 sin
sin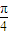 +2=2
+2=2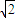 cos
cos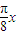 +2,
+2,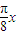 =-
=-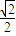 ,故
,故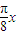 =2kπ±
=2kπ±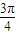 ,k∈z.
,k∈z.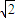 cos
cos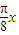 +2,是解题的关键,属于基础题.
+2,是解题的关键,属于基础题. 

 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:高中数学 来源: 题型:解答题
 已知函数
已知函数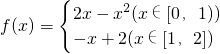 .
.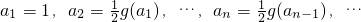 ,求数列{an}的通项公式;
,求数列{an}的通项公式;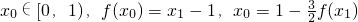 ,求x0和x1的值.
,求x0和x1的值.查看答案和解析>>
科目:高中数学 来源:2007-2008学年湖北省武汉市武昌区高一(上)期末数学模拟试卷(解析版) 题型:解答题
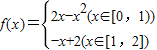 .
.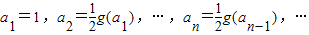 ,求数列{an}的通项公式;
,求数列{an}的通项公式;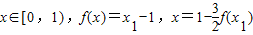 ,求x和x1的值.
,求x和x1的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
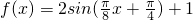 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com