
【题目】已知长方体ABCD﹣A1B1C1D1 , 下列向量的数量积一定不为0的是( )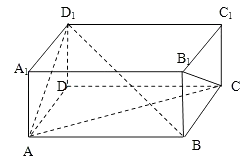
A.![]()
B.![]()
C.![]()
D.![]()
【答案】D
【解析】解:选项A,当四边形ADD1A1为正方形时,可得AD1⊥A1D,而A1D∥B1C,可得AD1⊥B1C,此时有 ![]() =0;
=0;
选项B,当四边形ABCD为正方形时,可得AC⊥BD,可得AC⊥平面BB1D1D,故有AC⊥BD1 , 此时有 ![]() =0;
=0;
选项C,由长方体的性质可得AB⊥平面ADD1A1 , 可得AB⊥AD1 , 此时必有 ![]() =0;
=0;
选项D,由长方体的性质可得BC⊥平面CDD1C1 , 可得BC⊥CD1 , △BCD1为直角三角形,∠BCD1为直角,
故BC与BD1不可能垂直,即 ![]() ≠0.
≠0.
故选:D
选项A,当四边形ADD1A1为正方形时,可证AD1⊥B1C,选项B,当四边形ABCD为正方形时,可证AC⊥BD1 , 选项C,由长方体的性质可证AB⊥AD1 , 分别可得数量积为0,选项D,可推在△BCD1中,∠BCD1为直角,可判BC与BD1不可能垂直,可得结论.


 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:
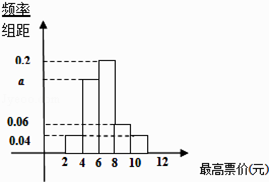
【题目】2014年5月,北京市提出地铁分段计价的相关意见,针对“你能接受的最高票价是多少?”这个问题,在某地铁站口随机对50人进行调查,调查数据的频率分布直方图及被调查者中35岁以下的人数与统计结果如下: (Ⅰ)根据频率分布直方图,求a的值,并估计众数,说明此众数的实际意义;
(Ⅱ)从“能接受的最高票价”落在[8,10),[10,12]的被调查者中各随机选取3人进行追踪调查,记选中的6人中35岁以上(含35岁)的人数为X,求随机变量X的分布列及数学期望.
最高票价 | 35岁以下人数 |
[2,4) | 2 |
[4,6) | 8 |
[6,8) | 12 |
[8,10) | 5 |
[10,12] | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大学生村官王善良落实政府“精准扶贫”精神,帮助贫困户张三用9万元购进一部节能环保汽车,用于出租.假设第一年需运营费用2万元,从第二年起,每年运营费用均比上一年增加2万元,该车每年的运营收入均为11万元.若该车使用了n(n∈N*)年后,年平均盈利额达到最大值,则n等于(注:年平盈利额=(总收入﹣总成本)× ![]() )( )
)( )
A.3
B.4
C.5
D.6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知P为△ABC所在平面外一点,PA⊥PB,PB⊥PC,PC⊥PA,PH⊥平面 ABC,H,则H为△ABC的( ) 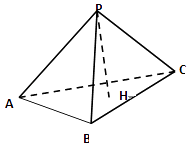
A.重心
B.垂心
C.外心
D.内心
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,过E点做EF⊥PB交PB于点F.求证: 
(1)PA∥平面DEB;
(2)PB⊥平面DEF.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,关于正方体ABCD﹣A1B1C1D1 , 下面结论错误的是( ) 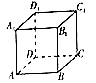
A.BD⊥平面ACC1A1
B.AC⊥BD
C.A1B∥平面CDD1C1
D.该正方体的外接球和内接球的半径之比为2:1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的偶函数f(x)的图象关于点(1,0)对称,且当x∈[1,2]时,f(x)=﹣2x+2,若函数y=f(x)﹣loga(|x|+1)恰好有8个零点,则实数a的取值范围是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com