
【题目】已知![]() 是由正整数组成的无穷数列,对任意
是由正整数组成的无穷数列,对任意![]() ,
,![]() 满足如下两个条件:①
满足如下两个条件:①![]() 是
是![]() 的倍数;②
的倍数;②![]() .
.
(1)若![]() ,
,![]() ,写出满足条件的所有
,写出满足条件的所有![]() 的值;
的值;
(2)求证:当![]() 时,
时,![]() ;
;
(3)求![]() 所有可能取值中的最大值.
所有可能取值中的最大值.
科目:高中数学 来源: 题型:
【题目】如图,某中学甲、乙两班共有25名学生报名参加了一项 测试.这25位学生的考分编成的茎叶图,其中有一个数据因电脑操作员不小心删掉了(这里暂用x来表示),但他清楚地记得两班学生成绩的中位数相同.

(Ⅰ)求这两个班学生成绩的中位数及x的值;
(Ⅱ)如果将这些成绩分为“优秀”(得分在175分 以上,包括175分)和“过关”,若学校再从这两个班获得“优秀”成绩的考生中选出3名代表学校参加比赛,求这3人中甲班至多有一人入选的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)已知sin(-π+θ)+2cos(3π-θ)=0,则![]() ;
;
(2)已知![]() .
.
①化简f(α);
②若f(α)![]() ,且
,且![]() ,求cos α-sin α的值;
,求cos α-sin α的值;
③若![]()
![]() ,求f(α)的值.
,求f(α)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
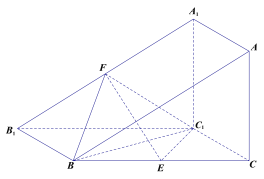
【题目】如图,三棱柱![]() 的侧面
的侧面![]() 是平行四边形,
是平行四边形,![]() ,平面
,平面![]() 平面
平面![]() ,且
,且![]() 分别是
分别是![]() 的中点.
的中点.
(1)求证:![]() 平面
平面![]() ;
;
(2)当侧面![]() 是正方形,且
是正方形,且![]() 时,
时,
(ⅰ)求二面角![]() 的大小;
的大小;
(ⅱ)在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ?若存在,指出点
?若存在,指出点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,
,![]() ,数列
,数列![]() 满足条件:对于
满足条件:对于![]() ,
,![]() ,且
,且![]() ,并有关系式:
,并有关系式:![]() ,又设数列
,又设数列![]() 满足
满足![]() (
(![]() 且
且![]() ,
,![]() ).
).
(1)求证数列![]() 为等比数列,并求数列
为等比数列,并求数列![]() 的通项公式;
的通项公式;
(2)试问数列![]() 是否为等差数列,如果是,请写出公差,如果不是,说明理由;
是否为等差数列,如果是,请写出公差,如果不是,说明理由;
(3)若![]() ,记
,记![]() ,
,![]() ,设数列
,设数列![]() 的前
的前![]() 项和为
项和为![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,若对任意的
,若对任意的![]() ,不等式
,不等式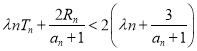 恒成立,试求实数
恒成立,试求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某射手每次射击击中目标的概率是![]() ,且各次射击的结果互不影响,假设这名射手射击3次.
,且各次射击的结果互不影响,假设这名射手射击3次.
(1)求恰有2次击中目标的概率;
(2)现在对射手的3次射击进行计分:每击中目标1次得1分,未击中目标得0分;若仅有2次连续击中,则额外加1分;若3次全击中,则额外加3分.记![]() 为射手射击3次后的总得分,求
为射手射击3次后的总得分,求![]() 的概率分布列与数学期望
的概率分布列与数学期望![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com