
分析 分别求解函数的值域和定义域化简集合A,B.
(1)把m=3代入集合B,然后利用补集与交集运算得答案;
(2)由A∩B=∅,得$\left\{\begin{array}{l}{m-3≤\frac{5}{2}}\\{m+3≥6}\end{array}\right.$,求解不等式组得答案.
解答 解:A={y|y=2x+2,x∈[-1,2]}=[$\frac{5}{2},6$],
由(x-m)2-9>0,得x<m-3或x>m+3.
∴B={x|y=lg[(x-m)2-9]}=(-∞,m-3)∪(m+3,+∞).
(1)若m=3,则B=(-∞,0)∪(6,+∞).
∁RA=($-∞,\frac{5}{2}$)∪(6,+∞),∁RB=[0,6].
∴(∁RA)∩(∁RB)=[0,$\frac{5}{2}$);
(2)若A∩B=∅,则$\left\{\begin{array}{l}{m-3≤\frac{5}{2}}\\{m+3≥6}\end{array}\right.$,解得:3$≤m≤\frac{11}{2}$.
点评 本题考查交、并、补集的运算,考查了函数的定义域及其值域的求法,是基础题.


 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 是奇函数 | B. | 是偶函数 | ||
| C. | 既是奇函数,又是偶函数 | D. | 既不是奇函数,又不是偶函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2016-2017学年云南大理州南涧县民族中学高二文9月月考数学试卷(解析版) 题型:选择题
设直线y=x+2a与圆C:x2+y2-2ay-2=0相交于A,B两点,若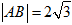 ,则圆C的内接正三角形的面积为( )
,则圆C的内接正三角形的面积为( )
A.4 B.8 C. 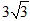 D.
D. 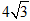
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com