
【题目】已知函数![]() ,曲线
,曲线![]() 在点
在点![]() ,
,![]() (1)
(1)![]() 处的切线方程为
处的切线方程为![]() .
.
(1)求函数![]() 的解析式,并证明:
的解析式,并证明:![]() .
.
(2)已知![]() ,且函数
,且函数![]() 与函数
与函数![]() 的图象交于
的图象交于![]() ,
,![]() ,
,![]() ,
,![]() 两点,且线段
两点,且线段![]() 的中点为
的中点为![]() ,
,![]() ,证明:
,证明:![]() (1)
(1)![]() .
.
【答案】(1)![]() ;证明见解析;(2)证明见解析;
;证明见解析;(2)证明见解析;
【解析】
(1)根据题意,对![]() 求导得
求导得![]() ,利用导数的几何意义和切线方程求出
,利用导数的几何意义和切线方程求出![]() 和
和![]() ,即可求出
,即可求出![]() 的解析式,令
的解析式,令![]() ,利用导数研究函数得单调性和最值得出
,利用导数研究函数得单调性和最值得出![]() ,即可证明不等式;
,即可证明不等式;
(2)结合分析法,把所要证明的问题转化为证明![]() ,设
,设![]() ,进而转化为只需证:
,进而转化为只需证:![]() ,构造函数
,构造函数![]() ,利用导数研究函数的单调性,从而可证明出
,利用导数研究函数的单调性,从而可证明出![]() (1)
(1)![]() .
.
解:(1)由题可知,![]() ,则
,则![]() ,
,
由于![]() 在点
在点![]() ,
,![]() (1)
(1)![]() 处的切线方程为
处的切线方程为![]() ,
,
所以![]() (1)
(1)![]() ,即
,即![]() ,
,
即![]() (1)
(1)![]() ,则
,则![]() ,解得:
,解得:![]() ,
,
则![]() .
.
令![]() ,
,![]() ,
,
令![]() ,即
,即![]() ,解得:
,解得:![]() ,
,
则![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;![]() 时,
时,![]() ,
,![]() 单调递增,
单调递增,
所以函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
![]() ,则
,则![]() .
.
(2)由题可知,![]() ,且
,且 ,
,
则![]() ,
,![]() ,
,
要证![]() (1)
(1)![]() 成立,
成立,
只需证:![]() ,
,
即证:![]() ,即证:
,即证:![]() ,
,
只需证:![]() ,
,
不妨设![]() ,即证:
,即证:![]() ,
,
要证![]() ,只需证:
,只需证:![]() ,
,
令![]() ,则
,则![]() ,
,
![]() 在
在![]() 上为增函数,
上为增函数,
![]() ,即
,即![]() 成立;
成立;
要证![]() ,只需证:
,只需证:![]() ,
,
令![]() ,则
,则![]() ,
,
![]() 在
在![]() 上为减函数,
上为减函数,
![]() ,即
,即![]() 成立.
成立.
![]()
![]() ,
,![]() 成立,
成立,
![]() (1)
(1)![]() 成立.
成立.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 经过点
经过点![]() 离心率
离心率![]() .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)经过椭圆左焦点![]() 的直线(不经过点
的直线(不经过点![]() 且不与
且不与![]() 轴重合)与椭圆交于
轴重合)与椭圆交于![]() 两点,与直线
两点,与直线![]() :
:![]() 交于点
交于点![]() ,记直线
,记直线![]() 的斜率分别为
的斜率分别为![]() .则是否存在常数
.则是否存在常数![]() ,使得向量
,使得向量![]()
![]() 共线?若存在求出
共线?若存在求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了增强学生的冬奥会知识,弘扬奥林匹克精神,北京市多所中小学校开展了模拟冬奥会各项比赛的活动.为了了解学生在越野滑轮和旱地冰壶两项中的参与情况,在北京市中小学学校中随机抽取了10所学校,10所学校的参与人数如下:
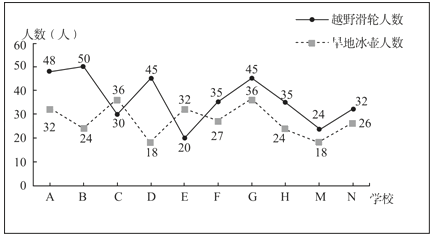
(Ⅰ)现从这10所学校中随机选取2所学校进行调查.求选出的2所学校参与越野滑轮人数都超过40人的概率;
(Ⅱ)现有一名旱地冰壶教练在这10所学校中随机选取2所学校进行指导,记X为教练选中参加旱地冰壶人数在30人以上的学校个数,求X的分布列和数学期望;
(Ⅲ)某校聘请了一名越野滑轮教练,对高山滑降、转弯、八字登坡滑行这3个动作进行技术指导.规定:这3个动作中至少有2个动作达到“优”,总考核记为“优”.在指导前,该校甲同学3个动作中每个动作达到“优”的概率为0.1.在指导后的考核中,甲同学总考核成绩为“优”.能否认为甲同学在指导后总考核达到“优”的概率发生了变化?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在现代社会中,信号处理是非常关键的技术,我们通过每天都在使用的电话或者互联网就能感受到,而信号处理背后的“功臣”就是正弦型函数.函数 的图象就可以近似的模拟某种信号的波形,则下列说法正确的是( )
的图象就可以近似的模拟某种信号的波形,则下列说法正确的是( )
A.函数![]() 为周期函数,且最小正周期为
为周期函数,且最小正周期为![]()
B.函数![]() 为奇函数
为奇函数
C.函数![]() 的图象关于直线
的图象关于直线![]() 对称
对称
D.函数![]() 的导函数
的导函数![]() 的最大值为
的最大值为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是数列1,
是数列1,![]() ,
,![]() ,…,
,…,![]() 的各项和,
的各项和,![]() ,
,![]() .
.
(1)设![]() ,证明:
,证明:![]() 在
在![]() 内有且只有一个零点;
内有且只有一个零点;
(2)当![]() 时,设存在一个与上述数列的首项、项数、末项都相同的等差数列,其各项和为
时,设存在一个与上述数列的首项、项数、末项都相同的等差数列,其各项和为![]() ,比较
,比较![]() 与
与![]() 的大小,并说明理由;
的大小,并说明理由;
(3)给出由公式![]() 推导出公式
推导出公式![]() 的一种方法如下:在公式
的一种方法如下:在公式![]() 中两边求导得:
中两边求导得:![]() ,所以
,所以![]() 成立,请类比该方法,利用上述数列的末项
成立,请类比该方法,利用上述数列的末项![]() 的二项展开式证明:
的二项展开式证明:![]() 时
时![]() (其中
(其中![]() 表示组合数)
表示组合数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】极坐标系与直角坐标系![]() 有相同的长度单位,以原点为极点,以
有相同的长度单位,以原点为极点,以![]() 轴正半轴为极轴,曲线
轴正半轴为极轴,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),射线
),射线![]() ,
,![]() ,
,![]() 与曲线
与曲线![]() 交于(不包括极点
交于(不包括极点![]() )三点
)三点![]() ,
,![]() ,
,![]() .
.
(1)求证:![]() ;
;
(2)当![]() 时,
时,![]() ,
,![]() 两点在曲线
两点在曲线![]() 上,求
上,求![]() 与
与![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,五边形![]() 中,四边形
中,四边形![]() 为长方形,
为长方形,![]() 为边长为
为边长为![]() 的正三角形,将
的正三角形,将![]() 沿
沿![]() 折起,使得点
折起,使得点![]() 在平面
在平面![]() 上的射影恰好在
上的射影恰好在![]() 上.
上.
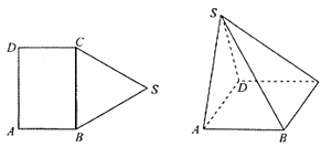
(Ⅰ)当![]() 时,证明:平面
时,证明:平面![]() 平面
平面![]() ;
;
(Ⅱ)若![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成二面角的余弦值的绝对值.
所成二面角的余弦值的绝对值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以直角坐标系的原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴,两个坐标系取相等的长度单位.已知圆
轴的正半轴为极轴,两个坐标系取相等的长度单位.已知圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
(1)求圆![]() 的普通方程和直线
的普通方程和直线![]() 的极坐标方程;
的极坐标方程;
(2)设圆![]() 和直线
和直线![]() 交于
交于![]() 两点,求
两点,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题![]()
![]() 的展开式中,仅有第7项的二项式系数最大,则展开式中的常数项为495;命题
的展开式中,仅有第7项的二项式系数最大,则展开式中的常数项为495;命题![]() 随机变量
随机变量![]() 服从正态分布
服从正态分布![]() ,且
,且![]() ,则
,则![]() .现给出四个命题:①
.现给出四个命题:①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() ,其中真命题的是( )
,其中真命题的是( )
A.①③B.①④C.②③D.②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com