
(本题14分,其中第(1)小题6分,第(2)小题8分)
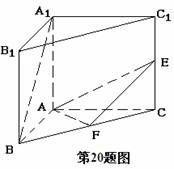 设在直三棱柱
设在直三棱柱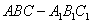 中,
中,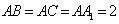 ,
,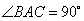 ,
, 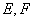 依次为
依次为 的中点.
的中点.
(1)求异面直线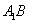 、
、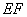 所成角
所成角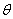 的大小(用反三角函数值表示);
的大小(用反三角函数值表示);
(2)求点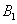 到平面
到平面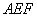 的距离.
的距离.
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案科目:高中数学 来源:上海市普陀区2010届高三第二次模拟考试理科数学试题 题型:解答题
(本题满分14分,其中第1小题8分,第2小题6分)
一企业生产的某产品在不做电视广告的前提下,每天销售量为 件. 经市场调查后得到如下规律:若对产品进行电视广告的宣传,每天的销售量
件. 经市场调查后得到如下规律:若对产品进行电视广告的宣传,每天的销售量 (件)与电视广告每天的播放量
(件)与电视广告每天的播放量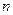 (次)的关系可用如图所示的程序框图来体现.
(次)的关系可用如图所示的程序框图来体现.
(1)试写出该产品每天的销 售量
售量 (件)关于电视广告每天的播放量
(件)关于电视广告每天的播放量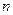 (次)的函数关系式;
(次)的函数关系式;
(2)要使该产品每天的销售量比不做电视广告时的销售量至少增加 ,则每天电视广告的播放量至少需多少次?
,则每天电视广告的播放量至少需多少次?
查看答案和解析>>
科目:高中数学 来源:2011-2012学年上海市高三模拟考试理科数学 题型:解答题
(本题满分14分,其中第1小题6分,第2小题8分)
为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建造隔热层.某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元.该建筑物每年的能源消耗费用 (单位:万元)与隔热层厚度
(单位:万元)与隔热层厚度 (单位:cm)满足关系:
(单位:cm)满足关系: ,若不建隔热层,每年能源消耗费用为8万元.设
,若不建隔热层,每年能源消耗费用为8万元.设 为隔热层建造费用与20年的能源消耗费用之和.
为隔热层建造费用与20年的能源消耗费用之和.
(1)求 的值及
的值及 的表达式;
的表达式;
(2)隔热层修建多厚时,总费用 达到最小,并求最小值.
达到最小,并求最小值.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年上海市高三模拟考试理科数学 题型:解答题
(本题满分14分,其中第1小题6分,第2小题8分)
在 中,
中,  分别为角
分别为角 的对边,且满足
的对边,且满足 .
.
(1)求角 大小;(2)若
大小;(2)若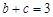 ,求
,求 的面积的最大值.
的面积的最大值.
查看答案和解析>>
科目:高中数学 来源:2010年上海市松江区高考模拟考试(理) 题型:解答题
(本题14分,其中第(1)小题8分,第(2)小题6分)
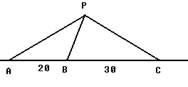 如图所示,在一条海防警戒线上的点
如图所示,在一条海防警戒线上的点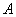 、
、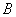 、
、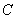 处各有一个水声监测点,
处各有一个水声监测点,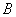 、
、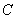 两点到点
两点到点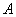 的距离分别为
的距离分别为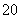 千米和
千米和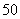 千米.某时刻,
千米.某时刻,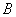 收到发自静止目标
收到发自静止目标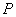 的一个声波信号,8秒后
的一个声波信号,8秒后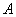 、
、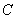 两点同时接收到该声波信号,已知声波在水中的传播速度是
两点同时接收到该声波信号,已知声波在水中的传播速度是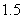 千米/秒.
千米/秒.
(1)设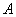 到
到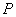 的距离为
的距离为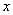 千米,用
千米,用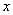 表示
表示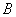 、
、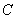 到
到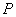 的距离,并求
的距离,并求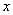 的值;
的值;
(2)求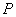 到海防警戒线
到海防警戒线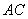 的距离(结果精确到
的距离(结果精确到 千米).
千米).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com