练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    通过随机询问110名不同的大学生是否爱好某项运动，得到如下的列联表：
     
    		男
    		女
    		总计
    爱好
    		40
    		20
    		60
    不爱好
    		20
    		30
    		50
    总计
    		60
    		50
    		110
    附： 

    		0．050
    		0．010
    		0．001

    		3．841
    		6．635
    		10．828
     
    试考查大学生“爱好该项运动是否与性别有关”，若有关，请说明有多少把握。
    有99%以上的把握认为“爱好该项运动与性别有关”.

    试题分析：由已知中判断爱好该项运动是否与性别有关时，由列联表中的数据此算得k2≈7.8，且7.8＞6.635，而P（k2≥6.635）≈0.01，故我们有99%的把握认为爱好该项运动与性别有关．则出错的可能性为1%.
    试题解析：由>6.635，所以有99%以上的把握认为“爱好该项运动与性别有关”。    12分‘
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：解答题

    某种水果的单个质量在500g以上视为特等品.随机抽取1000个该水果，结果有50个特等品.将这50个水果的质量数据分组，得到下边的频率分布表.

    （1）估计该水果的质量不少于560g的概率；
    （2）若在某批水果的检测中，发现有15个特等品，据此估计该批水果中没有达到特等品的个数.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    汽车的碳排放量比较大，某地规定，从2014年开始，将对二氧化碳排放量超过130g/km的轻型汽车进行惩罚性征税．检测单位对甲、乙两品牌轻型汽车各抽取5辆进行二氧化碳排放量检测，记录如下（单位：g/km）．

    经测算得乙品牌轻型汽车二氧化碳排放量的平均值为．
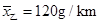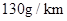    （1）从被检测的5辆甲品牌轻型汽车中任取2辆，则至少有一辆二氧化碳排放量超过的概率是多少？
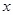    （2）求表中的值，并比较甲、乙两品牌轻型汽车二氧化碳排放量的稳定性．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    对一批产品的长度(单位: mm)进行抽样检测, 下图喂检测结果的频率分布直方图. 根据标准, 产品长度在区间[20,25)上的为一等品, 在区间[15,20)和区间[25,30)上的为二等品, 在区间[10,15)和[30,35)上的为三等品. 用频率估计概率, 现从该批产品中随机抽取一件, 则其为二等品的概率为
    A．0.09B．0.20C．0.25D．0.45

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    某公司为了了解员工们的健康状况，随机抽取了部分员工作为样本，测量他们的体重(单位:公斤)，体重的分组区间为[50,55),[55,60),[60,65),[65,70),[70,75]，由此得到样本的频率分布直方图，如图所示．根据频率分布直方图，估计该公司员工体重的众数是_____；从这部分员工中随机抽取1位员工，则该员工的体重在[65,75]的概率是_______．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    某校高三有四个班，某次数学测试后，学校随机地在各班抽取部分学生进行测试成绩统计，各班被抽取的学生人数恰好成等差数列，人数最少的班被抽取了22人. 抽取出来的所有学生的测试成绩统计结果的频率分布条形图如图所示，其中120~130（包括120分但不包括130分）的频率为0.05，此分数段的人数为5人.
    （1）问各班被抽取的学生人数各为多少人？
    （2）求平均成绩；
    （3）在抽取的所有学生中，任取一名学生，求分数不低于90分的概率.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    某企业有两个分厂生产某种零件，按规定内径尺寸(单位：mm)的值落在[29.94,30.06)的零件为优质品．从两个分厂生产的零件中各抽出了500件，量其内径尺寸，得结果如下表：
    甲厂：
    分组
    		[29.86，29.90)
    		[29.90，29.94)
    		[29.94，29.98)
    		[29.9830.02)，
    		[30.02，30.06)
    		[30.06，30.10)
    		[30.10，30.14)
    频数
    		12
    		63
    		86
    		182
    		92
    		61
    		4
    乙厂：
    分组
    		[29.86，29.90)
    		[29.90，29.94)
    		[29.94，29.98)
    		[29.9830.02)，
    		[30.02，30.06)
    		[30.06，30.10)
    		[30.10，30.14)
    频数
    		29
    		71
    		85
    		159
    		76
    		62
    		18
     
    (1)试分别估计两个分厂生产的零件的优质品率；
    (2)由以上统计数据填下面2×2列联表，并问是否有99%的把握认为“两个分厂生产的零件的质量有差异”？
     
    		甲厂
    		乙厂
    		合计
    优质品
    		 
    		 
    		 
    非优质品
    		 
    		 
    		 
    合　计
    		 
    		 
    		 
    附：
    P(χ2≥x0)
    		0.05
    		0.01
    x0
    		3.841
    		6.635
     

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    根据空气质量指数API(为整数)的不同,可将空气质量分级如下表:
    API
    		0～50
    		51～
    100
    		101～
    150
    		151～
    200
    		201～
    250
    		251～
    300
    		>300
    级　别
    		Ⅰ
    		Ⅱ
    		Ⅲ1
    		Ⅲ2
    		Ⅳ1
    		Ⅳ2
    		Ⅴ
    状　况
    		优
    		良
    		轻微
    污染
    		轻度
    污染
    		中度
    污染
    		中度
    重污染
    		重度
    污染
     





    对某城市一年(365天)的空气质量进行监测,获得的API数据按照区间[0,50],(50,100],(100,150],(150,200],(200,250],(250,300]进行分组,得到频率分布直方图如图.

    (1)求直方图中x的值.
    (2)计算一年中空气质量分别为良和轻微污染的天数.
    (3)求该城市某一周至少有2天的空气质量为良或轻微污染的概率.
    (结果用分数表示.
    已知57=78125,27=128,++++=,365=73×5).

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    某班班主任对全班50名学生学习积极性和对待班级工作的态度进行了调查，统计数据如下表所示．从表中数据分析，学生学习积极性与对待班级工作的态度之间有关系的把握有________.
     
    		积极参加班级工作
    		不太主动参加班级工作
    		合计
    学习积极性高
    		18
    		7
    		25
    学习积极性一般
    		6
    		19
    		25
    合计
    		24
    		26
    		50

    查看答案和解析>>

    同步练习册答案