
【题目】已知变量![]() ,
,![]() 满足下列条件:
满足下列条件: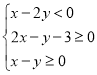 .
.
(1)求![]() 的最大值;
的最大值;
(2)求![]() 的最小值;
的最小值;
(3)求![]() 的最小值.
的最小值.
【答案】(1)无最大值.(2)无最小值.(3)最小值是3.
【解析】
根据题意作出可行域
(1)将![]() 改写成
改写成![]() ,即
,即![]() 为直线在
为直线在![]() 轴上的截距,根据可行域可得出结论.
轴上的截距,根据可行域可得出结论.
(2)直线![]() ,变形为
,变形为![]() .问题转而求直线在
.问题转而求直线在![]() 轴上截距的最小值.根据可行域可得出结论.
轴上截距的最小值.根据可行域可得出结论.
(3)![]() 写成
写成![]() .即先求直线在
.即先求直线在![]() 轴上截距
轴上截距![]() 的最大值,从而求出
的最大值,从而求出![]() 的最小值,几何可行域可得出答案.
的最小值,几何可行域可得出答案.
解 如图所示,画出直线![]() (虚线);
(虚线);![]() (实线);
(实线);![]() (实线).
(实线).
则不等式组满足的平面区域如图所示的阴影部分.
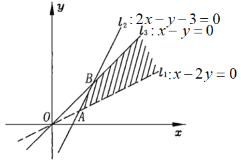
(1)将![]() 改写成
改写成![]() ,即
,即![]() 为直线在
为直线在![]() 轴上的截距,
轴上的截距,
求![]() 的最大值即求直线
的最大值即求直线![]() 在
在![]() 轴上截距的最大值.
轴上截距的最大值.
由于满足条件的平面区域不是封闭的.![]() 和
和![]() 的取值均无上界,故直线在
的取值均无上界,故直线在![]() 轴上截距无最大值,即
轴上截距无最大值,即![]() 无最大值.
无最大值.
(2)直线![]() ,同理变形为
,同理变形为![]() .问题转而求直线在
.问题转而求直线在![]() 轴上截距的最小值.
轴上截距的最小值.
当直线过![]() 时看似取最小值,但点
时看似取最小值,但点![]() 不包括在平面区域内,故
不包括在平面区域内,故![]() 也无最小值.
也无最小值.
(3)![]() 写成
写成![]() .即先求直线在
.即先求直线在![]() 轴上截距
轴上截距![]() 的最大值,从而求出
的最大值,从而求出![]() 的最小值.
的最小值.
由![]() 可得点
可得点![]() 坐标为
坐标为![]() ,
,
作直线![]() .平移
.平移![]() 可知
可知![]() 过点
过点![]() 时,直线在
时,直线在![]() 轴上截距
轴上截距![]() 最大,即此时
最大,即此时![]() 最小.
最小.
将![]() 代入,得
代入,得![]() ,
,
所以![]() 的最小值是3.
的最小值是3.


科目:高中数学 来源: 题型:
【题目】某单位一辆交通车载有8个职工从单位出发送他们下班回家,途中共有甲、乙、丙3个停车点.如果某停车点无人下车,那么该车在这个点就不停车.假设每个职工在每个停车点下车的可能性都是相等的,求下列事件的概率:
(1)该车在某停车点停车;
(2)停车的次数不少于2次;
(3)恰好停车2次.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙三台机床各自独立地加工同一种零件,已知甲机床加工的零件是一等品而乙机床加工的零件不是一等品的概率为![]() ,乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率为
,乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率为![]() ,甲、丙两台机床加工的零件都是一等品的概率为
,甲、丙两台机床加工的零件都是一等品的概率为![]() .
.
(1)分别求甲、乙、丙三台机床各自加工的零件是一等品的概率;
(2)从甲、乙、丙加工的零件中各取一个检验,求至少有一个一等品的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在矩形ABCD中,![]() ,
,![]() ,沿矩形对角线BD将
,沿矩形对角线BD将![]() 折起形成四面体ABCD,在这个过程中,现在下面四个结论:①在四面体ABCD中,当
折起形成四面体ABCD,在这个过程中,现在下面四个结论:①在四面体ABCD中,当![]() 时,
时,![]() ;②四面体ABCD的体积的最大值为
;②四面体ABCD的体积的最大值为![]() ;③在四面体ABCD中,BC与平面ABD所成角可能为
;③在四面体ABCD中,BC与平面ABD所成角可能为![]() ;④四面体ABCD的外接球的体积为定值.其中所有正确结论的编号为( )
;④四面体ABCD的外接球的体积为定值.其中所有正确结论的编号为( )
A.①④B.①②C.①②④D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随机抽取一个年份,对西安市该年4月份的天气情况进行统计,结果如下:
日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
天气 | 晴 | 雨 | 阴 | 阴 | 阴 | 雨 | 阴 | 晴 | 晴 | 晴 | 阴 | 晴 | 晴 | 晴 | 晴 |
日期 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
天气 | 晴 | 阴 | 雨 | 阴 | 阴 | 晴 | 阴 | 晴 | 晴 | 晴 | 阴 | 晴 | 晴 | 晴 | 雨 |
(1)在4月份任取一天,估计西安市在该天不下雨的概率;
(2)西安市某学校拟从4月份的一个晴天开始举行连续2天的运动会,估计运动会期间不下雨的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com