
【题目】已知函数f(x)=ex+2ax(a为常数)的图象与y轴交于点A,曲线y=f(x)在点A处的切线斜率为﹣1.
(1)求a的值及函数f(x)的极值;
(2)证明:当x>0时,x2+1<ex .
【答案】
(1)解:由f(x)=ex+2ax,得f'(x)=ex+2a,
令x=0,可得f(0)=1,
可得y=f(x)在点A(0,1)处的切线斜率为e0+2a=﹣1,
即2a=﹣2,解得a=﹣1;
f(x)=ex﹣2x,f′(x)=ex﹣2,
当x>ln2时,可得f′(x)>0,f(x)递增;
当x<ln2时,可得f′(x)<0,f(x)递减.
即有f(x)在x=ln2处,取得极小值,
且为2﹣2ln2,无极大值;
(2)证明:令g(x)=ex﹣x2﹣1,
则g'(x)=ex﹣2x,
由(Ⅰ)得,g(x)在x=ln2处,取得极小值,
且为最小值2﹣2ln2,
由2﹣2ln2>0,
即有g′(x)>0,
则g(x)在(0,+∞)递增,
可得g(x)>g(0)=0,
即当x>0时,x2+1<ex.
【解析】(1)求得f(x)的导数,求得点A(0,1),可得切线的斜率,解方程可得a=﹣1;由导数大于0,可得增区间;导数小于0,可得减区间,进而得到极小值,无极大值;(2)令g(x)=ex﹣x2﹣1,求出导数,再由(Ⅰ)可得g′(x)>0,则g(x)在(0,+∞)递增,即可得证.
【考点精析】解答此题的关键在于理解函数的极值与导数的相关知识,掌握求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值.
是极小值.


科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的前n项和为Sn , 公差d≠0,且S3+S5=50,a1 , a4 , a13成等比数列.
(1)求数列{an}的通项公式;
(2)设{ ![]() }是首项为1公比为2的等比数列,求数列{bn}前n项和Tn .
}是首项为1公比为2的等比数列,求数列{bn}前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四边形ABCD中,△ABC是边长为6的正三角形,设 ![]() (x,y∈R).
(x,y∈R). 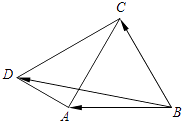
(1)若x=y=1,求| ![]() |;
|;
(2)若 ![]() =36,
=36, ![]() =54,求x,y.
=54,求x,y.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】参加衡水中学数学选修课的同学,对某公司的一种产品销量与价格进行统计,得到如下数据和散点图:
定价 |
|
|
|
|
|
|
年销售 |
|
|
|
|
|
|
|
|
|
|
|
|
|
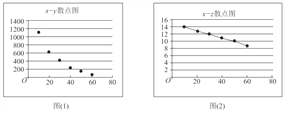
(参考数据:![]()
![]() )
)
(I)根据散点图判断,![]() 与
与![]() ,
,![]() 与
与![]() 哪一对具有较强的线性相关性(给出判断即可,不必说明理由)?
哪一对具有较强的线性相关性(给出判断即可,不必说明理由)?
(II)根据(I)的判断结果有数据,建立![]() 关于
关于![]() 的回归方程(方程中的系数均保留两位有效数字);
的回归方程(方程中的系数均保留两位有效数字);
(III)定价为多少元/![]() 时,年利润的预报值最大?
时,年利润的预报值最大?
附:对一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: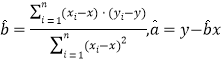 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求M在AB的延长线上,N在AD的延长线上,且对角线MN过点C,已知AB=3米,AD=2米,记矩形AMPN的面积为S平方米. 
(1)按下列要求建立函数关系;
(i)设AN=x米,将S表示为x的函数;
(ii)设∠BMC=θ(rad),将S表示为θ的函数.
(2)请你选用(1)中的一个函数关系,求出S的最小值,并求出S取得最小值时AN的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】政府鼓励创新、创业,银行给予低息贷款.一位大学毕业生向自主创业,经过市场调研、测算,有两个方案可供选择.
方案1:开设一个科技小微企业,需要一次性贷款40万元,第一年获利是贷款额的10%,以后每年比上一年增加25%的利润.
方案2:开设一家食品小店,需要一次性贷款20万元,第一年获利是贷款额的15%,以后每年比上一年增加利润1.5万元.两种方案使用期限都是10年,到期一次性还本付息.两种方案均按年息2%的复利计算(参考数据:1.259=7.45,1.2510=9.3,1.029=1.20,1.0210=1.22).
(1)10年后,方案1,方案2的总收入分别有多少万元?
(2)10年后,哪一种方案的利润较大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017安徽阜阳二模】一企业从某生产线上随机抽取![]() 件产品,测量这些产品的某项技术指标值
件产品,测量这些产品的某项技术指标值![]() ,得到的频率分布直方图如图.
,得到的频率分布直方图如图.
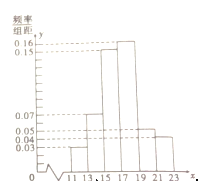
(1)估计该技术指标值![]() 平均数
平均数![]() ;
;
(2)在直方图的技术指标值分组中,以![]() 落入各区间的频率作为
落入各区间的频率作为![]() 取该区间值的频率,若
取该区间值的频率,若![]() ,则产品不合格,现该企业每天从该生产线上随机抽取
,则产品不合格,现该企业每天从该生产线上随机抽取![]() 件产品检测,记不合格产品的个数为
件产品检测,记不合格产品的个数为![]() ,求
,求![]() 的数学期望
的数学期望![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com