已知a∈R,函数f(x)=(-x2+ax)e-x(x∈R,e为自然对数的底数).
(I)当a=-2时,求函数,f(x)的单调递减区间;
(Ⅱ)若函数f(x)在(-1,1)内单调递减,求a的取值范围;
(III)函数f(x)是否为R上的单调函数,若是,求出a的取值范围:若不是,请说明理由.
解:(Ⅰ)当a=-2时,f(x)=(-x
2-2x)e
-x;f′(x)=(x
2-2)e
-x令f′(x)<0,得x
2-2<0,∴-

<x<

∴f(x)的单调递减区间是(-

,

);
(Ⅱ)f′(x)=[x
2-(a+2)x+a]e
-x,若f(x)在(-1,1)内单调递减,即当-1<x<1时,f′(x)≤0,
即x
2-(a+2)x+a≤0对x∈(-1,1)恒成立;
令g(x)=x
2-(a+2)x+a,则
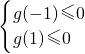
∴

,解得a≤-

;
(III)f′(x)=[x
2-(a+2)x+a]e
-x,其正负取决于二次式x
2-(a+2)x+a,该二次式值(首项为正)不可能永为负,也就是说原函数不可能是整个实数域上的单调递减函数;
若要成为单调递增函数,则x
2-(a+2)x+a≥0对x∈R恒成立
∵△=(a+2)
2-4a=a
2+4>0
∴函数不可能在R上单调递增
综上可知,函数f(x)不可能为R上的单调函数.
分析:(Ⅰ)求导函数,令f′(x)<0,可得f(x)的单调递减区间;
(Ⅱ)f′(x)=[x
2-(a+2)x+a]e
-x,若f(x)在(-1,1)内单调递减,即当-1<x<1时,f′(x)≤0,即x
2-(a+2)x+a≤0对x∈(-1,1)恒成立,变换主元,可得不等式组,从而可求a的值;
(III)判断函数不可能是整个实数域上的单调递减函数;要成为单调递增函数,则x
2-(a+2)x+a≥0对x∈R恒成立,判断其不可能,即可得到结论.
点评:本题考查导数知识的运用,考查函数的单调性,考查学生分析解决问题的能力,属于中档题.

 <x<
<x<
 ,
, );
);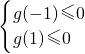
 ,解得a≤-
,解得a≤- ;
;
