
ЁОЬтФПЁПгавЛЦЌВњСПКмДѓЕФЫЎЙћжжжВдАЃЌдкСйНќГЩЪьЪБЫцЛњеЊЯТФГЦЗжжЫЎЙћ100ИіЃЌЦфжЪСПЃЈОљдкlжС11kgЃЉЦЕЪ§ЗжВМБэШчЯТЃЈЕЅЮЛ: kgЃЉЃК
Зжзщ | | | | | |
ЦЕЪ§ | 10 | 15 | 45 | 20 | 10 |
вдИїзщЪ§ОнЕФжаМфжЕДњБэетзщЪ§ОнЕФЦНОљжЕЃЌНЋЦЕТЪЪгЮЊИХТЪ.
ЃЈ1ЃЉгЩжжжВОбщШЯЮЊЃЌжжжВдАФкЕФЫЎЙћжЪСП![]() НќЫЦЗўДге§ЬЌЗжВМ
НќЫЦЗўДге§ЬЌЗжВМ![]() ЃЌЦфжа
ЃЌЦфжа![]() НќЫЦЮЊбљБОЦНОљЪ§
НќЫЦЮЊбљБОЦНОљЪ§![]() НќЫЦЮЊбљБОЗНВю
НќЫЦЮЊбљБОЗНВю![]() .ЧыЙРЫуИУжжжВдАФкЫЎЙћжЪСПдк
.ЧыЙРЫуИУжжжВдАФкЫЎЙћжЪСПдк![]() ФкЕФАйЗжБШЃЛ
ФкЕФАйЗжБШЃЛ
ЃЈ2ЃЉЯждкДгжЪСПЮЊ![]() ЕФШ§зщЫЎЙћжагУЗжВуГщбљЗНЗЈГщШЁ14ИіЫЎЙћЃЌдйДгет14ИіЫЎЙћжаЫцЛњГщШЁ3ИіЃЎШєЫЎЙћжЪСП
ЕФШ§зщЫЎЙћжагУЗжВуГщбљЗНЗЈГщШЁ14ИіЫЎЙћЃЌдйДгет14ИіЫЎЙћжаЫцЛњГщШЁ3ИіЃЎШєЫЎЙћжЪСП![]() ЕФЫЎЙћУПЯњЪлвЛИіЫљЛёЕУЕФЕФРћШѓЗжБ№ЮЊ2дЊЃЌ4дЊЃЌ6дЊЃЌМЧЫцЛњГщШЁЕФ3ИіЫЎЙћзмРћШѓЮЊ
ЕФЫЎЙћУПЯњЪлвЛИіЫљЛёЕУЕФЕФРћШѓЗжБ№ЮЊ2дЊЃЌ4дЊЃЌ6дЊЃЌМЧЫцЛњГщШЁЕФ3ИіЫЎЙћзмРћШѓЮЊ![]() дЊЃЌЧѓ
дЊЃЌЧѓ![]() ЕФЗжВМСаМАЪ§бЇЦкЭћ.
ЕФЗжВМСаМАЪ§бЇЦкЭћ.
ИНЃК![]()
![]() ЃЌдђ
ЃЌдђ![]() .
.
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉМћНтЮі
ЃЛЃЈ2ЃЉМћНтЮі
ЁОНтЮіЁП
ЃЈ1ЃЉЧѓГі![]() ЃН6.1ЃЌгЩе§ЬЌЗжВМжЊPЃЈ4ЃМZЃМ8.2ЃЉЃНPЃЈІЬЉІвЃМZЃМІЬ+ІвЃЉЃН0.6826ЃЌМДПЩЕУД№АИЃЎ
ЃН6.1ЃЌгЩе§ЬЌЗжВМжЊPЃЈ4ЃМZЃМ8.2ЃЉЃНPЃЈІЬЉІвЃМZЃМІЬ+ІвЃЉЃН0.6826ЃЌМДПЩЕУД№АИЃЎ
ЃЈ2ЃЉІЮЕФПЩФмШЁжЕЮЊЃК8ЃЌ10ЃЌ12ЃЌ14ЃЌ16ЃЌ18ЃЌЗжБ№ЧѓГіЯргІЕФИХТЪЃЌгЩДЫФмЧѓГіІЮЕФЗжВМСаКЭЪ§бЇЦкЭћЃЎ
ЃЈ1ЃЉ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
![]() НќЫЦЮЊ
НќЫЦЮЊ![]() ЃЌ
ЃЌ![]() ЃЌгЩе§ЬЌЗжВМ
ЃЌгЩе§ЬЌЗжВМ![]() ЃЌ
ЃЌ
ЫљвдИУжжжВдАФкЫЎЙћжЪСПдк![]() ФкЕФАйЗжБШЮЊ
ФкЕФАйЗжБШЮЊ![]() .
.
ЃЈ2ЃЉ![]() ЕФПЩФмШЁжЕЮЊЃК8,10,12,14,16ЃЌ18.
ЕФПЩФмШЁжЕЮЊЃК8,10,12,14,16ЃЌ18.
![]() ЃЛ
ЃЛ
![]() ЃЛ
ЃЛ
![]() ЃЛ
ЃЛ
![]() ЃЛ
ЃЛ
![]() ЃЛ
ЃЛ
![]() ЃЛ
ЃЛ
ЗжВМСаЮЊ
| 8 | 10 | 12 | 14 | 16 | 18 |
| | | | | | |
![]() .
.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЫФУцЬх![]() жаЃЌEЪЧЯпЖЮ
жаЃЌEЪЧЯпЖЮ![]() ЕФжаЕуЃЌ
ЕФжаЕуЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() .
.

ЃЈ1ЃЉжЄУїЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЧѓЦНУц![]() гыЦНУц
гыЦНУц![]() ЫљГЩШёЖўУцНЧЕФгрЯвжЕ.
ЫљГЩШёЖўУцНЧЕФгрЯвжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌвбжЊ
ЃЌвбжЊ![]() ЃЌ
ЃЌ![]() ЗжБ№ЪЧ
ЗжБ№ЪЧ![]() ЃЌ
ЃЌ![]() ЕФжаЕуЃЌНЋ
ЕФжаЕуЃЌНЋ![]() би
би![]() елЦ№ЃЌЪЙ
елЦ№ЃЌЪЙ![]() ЕН
ЕН![]() ЕФЮЛжУШчЭМЫљЪОЃЌЧв
ЕФЮЛжУШчЭМЫљЪОЃЌЧв![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ

ЃЈ1ЃЉЧѓжЄЃКЦНУц![]() ЦНУц
ЦНУц![]() ЃЎ
ЃЎ
ЃЈ2ЃЉЧѓЦНУц![]() гыЦНУц
гыЦНУц![]() ЫљГЩШёЖўУцНЧЕФДѓаЁЃЎ
ЫљГЩШёЖўУцНЧЕФДѓаЁЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃИпШ§ФаЩњЬхг§ПЮЩЯзіЭЖРКЧђгЮЯЗЃЌСНШЫвЛзщЃЌУПТжгЮЯЗжаЃЌУПаЁзщСНШЫУПШЫЭЖРКСНДЮЃЌЭЖРКЭЖНјЕФДЮЪ§жЎКЭВЛЩйгк![]() ДЮГЦЮЊЁАгХауаЁзщЁБ.аЁУїгыаЁССЭЌвЛаЁзщЃЌаЁУїЁЂаЁССЭЖРКЭЖНјЕФИХТЪЗжБ№ЮЊ
ДЮГЦЮЊЁАгХауаЁзщЁБ.аЁУїгыаЁССЭЌвЛаЁзщЃЌаЁУїЁЂаЁССЭЖРКЭЖНјЕФИХТЪЗжБ№ЮЊ![]() .
.
ЃЈ1ЃЉШє![]() ЃЌ
ЃЌ![]() ЃЌдђдкЕквЛТжгЮЯЗЫћУЧЛёЁАгХауаЁзщЁБЕФИХТЪЃЛ
ЃЌдђдкЕквЛТжгЮЯЗЫћУЧЛёЁАгХауаЁзщЁБЕФИХТЪЃЛ
ЃЈ2ЃЉШє![]() дђгЮЯЗжааЁУїаЁССаЁзщвЊЯыЛёЕУЁАгХауаЁзщЁБДЮЪ§ЮЊ
дђгЮЯЗжааЁУїаЁССаЁзщвЊЯыЛёЕУЁАгХауаЁзщЁБДЮЪ§ЮЊ![]() ДЮЃЌдђРэТлЩЯжСЩйвЊНјааЖрЩйТжгЮЯЗВХааЃПВЂЧѓДЫЪБ
ДЮЃЌдђРэТлЩЯжСЩйвЊНјааЖрЩйТжгЮЯЗВХааЃПВЂЧѓДЫЪБ![]() ЕФжЕ.
ЕФжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЧњЯп![]() ЕФМЋзјБъЗНГЬЮЊ
ЕФМЋзјБъЗНГЬЮЊ![]() ЃЌжБЯп
ЃЌжБЯп![]() ЃК
ЃК![]() ЃЌжБЯп
ЃЌжБЯп![]() ЃК
ЃК![]() ЃЎвдМЋЕу
ЃЎвдМЋЕу![]() ЮЊдЕуЃЌМЋжсЮЊ
ЮЊдЕуЃЌМЋжсЮЊ![]() жсЕФе§АыжсНЈСЂЦНУцжБНЧзјБъЯЕЃЎ
жсЕФе§АыжсНЈСЂЦНУцжБНЧзјБъЯЕЃЎ
ЃЈ1ЃЉЧѓжБЯп![]() ЃЌ
ЃЌ![]() ЕФжБНЧзјБъЗНГЬвдМАЧњЯп
ЕФжБНЧзјБъЗНГЬвдМАЧњЯп![]() ЕФВЮЪ§ЗНГЬЃЛ
ЕФВЮЪ§ЗНГЬЃЛ
ЃЈ2ЃЉвбжЊжБЯп![]() гыЧњЯп
гыЧњЯп![]() НЛгк
НЛгк![]() ЃЌ
ЃЌ![]() СНЕуЃЌжБЯп
СНЕуЃЌжБЯп![]() гыЧњЯпCНЛгк
гыЧњЯпCНЛгк![]() ЃЌ
ЃЌ![]() СНЕуЃЌЧѓ
СНЕуЃЌЧѓ![]() ЕФУцЛ§ЃЎ
ЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЭждВ![]() ЕФЫФИіЖЅЕуЮЇГЩЕФСтаЮЕФУцЛ§ЮЊ
ЕФЫФИіЖЅЕуЮЇГЩЕФСтаЮЕФУцЛ§ЮЊ![]() ЃЌЭждВЕФвЛИіНЙЕуЮЊ
ЃЌЭждВЕФвЛИіНЙЕуЮЊ![]() .
.
ЃЈ1ЃЉЧѓЭждВЕФЗНГЬЃЛ
ЃЈ2ЃЉШє![]() ЃЌ
ЃЌ![]() ЮЊЭждВЩЯЕФСНИіЖЏЕуЃЌжБЯп
ЮЊЭждВЩЯЕФСНИіЖЏЕуЃЌжБЯп![]() ЃЌ
ЃЌ![]() ЕФаБТЪЗжБ№ЮЊ
ЕФаБТЪЗжБ№ЮЊ![]() ЃЌ
ЃЌ![]() ЃЌЕБ
ЃЌЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЕФУцЛ§ЪЧЗёЮЊЖЈжЕЃПШєЮЊЖЈжЕЃЌЧѓГіДЫЖЈжЕЃЛШєВЛЮЊЖЈжЕЃЌЫЕУїРэгЩ.
ЕФУцЛ§ЪЧЗёЮЊЖЈжЕЃПШєЮЊЖЈжЕЃЌЧѓГіДЫЖЈжЕЃЛШєВЛЮЊЖЈжЕЃЌЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПДгФГЦѓвЕЩњВњЕФФГжжВњЦЗжаГщШЁ100МўЃЌВтСПетаЉВњЦЗЕФвЛЯюжЪСПжИБъжЕЃЌгЩВтСПНсЙћЕУШчЯТЦЕТЪЗжВМжБЗНЭМЃК

ЃЈ1ЃЉЧѓет100МўВњЦЗжЪСПжИБъжЕЕФбљБОЦНОљЪ§![]() КЭбљБОЗНВю
КЭбљБОЗНВю![]() ЃЈЭЌвЛзщЕФЪ§ОнгУИУзщЧјМфЕФжаЕужЕзїЮЊДњБэЃЉЃЛ
ЃЈЭЌвЛзщЕФЪ§ОнгУИУзщЧјМфЕФжаЕужЕзїЮЊДњБэЃЉЃЛ
ЃЈ2ЃЉгЩжБЗНЭМПЩвдШЯЮЊЃЌетжжВњЦЗЕФжЪСПжИБъжЕ![]() ЗўДге§ЬЌЗжВМ
ЗўДге§ЬЌЗжВМ![]() ЃЌЦфжа
ЃЌЦфжа![]() НќЫЦЮЊбљБОЦНОљЪ§
НќЫЦЮЊбљБОЦНОљЪ§![]() ЃЌ
ЃЌ![]() НќЫЦЮЊбљБОЗНВю
НќЫЦЮЊбљБОЗНВю![]() ЁЃ
ЁЃ
ЃЈiЃЉШєФГгУЛЇДгИУЦѓвЕЙКТђСЫ10МўетжжВњЦЗЃЌМЧ![]() БэЪОет10МўВњЦЗжажЪСПжИБъжЕЮЛгкЃЈ187.4ЃЌ225.2ЃЉЕФВњЦЗМўЪ§ЃЌЧѓ
БэЪОет10МўВњЦЗжажЪСПжИБъжЕЮЛгкЃЈ187.4ЃЌ225.2ЃЉЕФВњЦЗМўЪ§ЃЌЧѓ![]() ЃЛ
ЃЛ
ЃЈiiЃЉвЛЬьФкГщШЁЕФВњЦЗжаЃЌШєГіЯжСЫжЪСПжИБъжЕдк![]() жЎЭтЕФВњЦЗЃЌОЭШЯЮЊетвЛЬьЕФЩњВњЙ§ГЬжаПЩФмГіЯжСЫвьГЃЧщПіЃЌашЖдЕБЬьЕФЩњВњЙ§ГЬНјааМьВщЯТЁЃЯТУцЕФОЅвЖЭМЪЧМьбщдБдквЛЬьФкГщШЁЕФ15ИіВњЦЗЕФжЪСПжИБъжЕЃЌИљОнНќЫЦжЕХаЖЯЪЧЗёашвЊЖдЕБЬьЕФЩњВњЙ§ГЬНјааМьВщЁЃ
жЎЭтЕФВњЦЗЃЌОЭШЯЮЊетвЛЬьЕФЩњВњЙ§ГЬжаПЩФмГіЯжСЫвьГЃЧщПіЃЌашЖдЕБЬьЕФЩњВњЙ§ГЬНјааМьВщЯТЁЃЯТУцЕФОЅвЖЭМЪЧМьбщдБдквЛЬьФкГщШЁЕФ15ИіВњЦЗЕФжЪСПжИБъжЕЃЌИљОнНќЫЦжЕХаЖЯЪЧЗёашвЊЖдЕБЬьЕФЩњВњЙ§ГЬНјааМьВщЁЃ
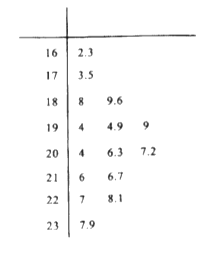
ИНЃК![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЭждВ![]() ЃК
ЃК![]() ЕФзѓгвНЙЕуЗжБ№ЮЊ
ЕФзѓгвНЙЕуЗжБ№ЮЊ![]() ЃЌ
ЃЌ![]() ЃЌРыаФТЪЮЊ
ЃЌРыаФТЪЮЊ![]() ЃЌЙ§
ЃЌЙ§![]() ЕФжБЯп
ЕФжБЯп![]() гыЭждВ
гыЭждВ![]() НЛгк
НЛгк![]() ЃЌ
ЃЌ![]() СНЕуЃЌЧв
СНЕуЃЌЧв![]() жмГЄЮЊ8.
жмГЄЮЊ8.
ЃЈ1ЃЉЧѓЭждВ![]() ЕФБъзМЗНГЬЃЛ
ЕФБъзМЗНГЬЃЛ
ЃЈ2ЃЉЪЧЗёДцдкжБЯп![]() ЃЌЪЙвд
ЃЌЪЙвд![]() ЮЊжБОЖЕФдВОЙ§зјБъдЕу
ЮЊжБОЖЕФдВОЙ§зјБъдЕу![]() ЃЌШєДцдкЧѓГіжБЯп
ЃЌШєДцдкЧѓГіжБЯп![]() ЕФЗНГЬЃЛШєВЛДцдкЃЌЫЕУїРэгЩ.
ЕФЗНГЬЃЛШєВЛДцдкЃЌЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЦНаажОдИЭЖЕЕТМШЁФЃЪНЪЧИпПМжОдИЕФвЛжжаТЗНЪНЃЌ2008ФъНЬг§ВПдк6ИіЪЁЧјЪЕааЦНаажОдИЭЖЕЕТМШЁФЃЪНЕФЪдЕуИФИя.вЛФъЕФЪЕМљжЄпЖЃЌЪЕааЦНаажОдИЭЖЕЕТМШЁФЃЪНЃЌгааЇНЕЕЭСЫПМЩњжОдИЬюБЈЗчЯе.ЦНаажОдИЪЧетбљЙцЖЈЃКдкЭЌвЛХњДЮЩшжУМИИіжОдИЃЌЕБПМЩњЗжЪ§ДяЕНетМИИібЇаЃЬсЕЕЯпЪБЃЌБОХњДЮЕФжОдИвРДЮМьЫїТМШЁ.ФГПМЩњИљОнЖдздМКЕФИпПМЗжЪ§КЭЖдЭљФъбЇаЃТМШЁЧщПіЗжЮіЃЌДгБЈПМжИФЯжабЁдёСЫ10ЫљбЇаЃЃЌзїГіШчЯТБэИёЃК
бЇаЃ |
|
|
|
|
|
|
|
|
|
|
зЈвЕ | Ъ§бЇЯЕ | МЦЫуЛњЯЕ | ЮяРэЯЕ | |||||||
ТМШЁИХТЪ | 0.5 | 0.5 | 0.6 | 0.9 | 0.5 | 0.7 | 0.8 | 0.7 | 0.8 | 0.9 |
ЃЈ1ЃЉИУПМЩњДгЩЯБэжаЕФ10ЫљбЇаЃжабЁдё4ЫљбЇаЃЬюБЈЃЌМЧ![]() ЮЊбЁдёЕФ4ЫљбЇаЃжаБЈЪ§бЇЯЕзЈвЕЕФИіЪ§ЃЌЧѓ
ЮЊбЁдёЕФ4ЫљбЇаЃжаБЈЪ§бЇЯЕзЈвЕЕФИіЪ§ЃЌЧѓ![]() ЕФЗжВМСаМАЦфЦкЭћ
ЕФЗжВМСаМАЦфЦкЭћ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШєИУПМЩњбЁдёСЫ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ет4ИібЇаЃдкЭЌвЛХњДЮЬюБЈжОдИЃЌЬюБЈжОдИБэШчЯТЃЌШчЙћНівдИУПМЩњЖдздМКЗжЮіЕФТМШЁИХТЪЮЊвРОнЃЌЕБИФБфет4ИіжОдИЬюБЈЕФЫГађЪБЃЌЪЧЗёИФБфЫћБОХњДЮТМШЁЕФПЩФмадЃПЧыЫЕУїРэгЩ.
ет4ИібЇаЃдкЭЌвЛХњДЮЬюБЈжОдИЃЌЬюБЈжОдИБэШчЯТЃЌШчЙћНівдИУПМЩњЖдздМКЗжЮіЕФТМШЁИХТЪЮЊвРОнЃЌЕБИФБфет4ИіжОдИЬюБЈЕФЫГађЪБЃЌЪЧЗёИФБфЫћБОХњДЮТМШЁЕФПЩФмадЃПЧыЫЕУїРэгЩ.
жОдИ | бЇаЃ |
ЕквЛжОдИ | |
ЕкЖўжОдИ | |
ЕкШ§жОдИ | |
ЕкЫФжОдИ |
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com