
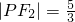 .
. ,
,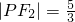 ,利用抛物线的定义可得xP-(-1)=
,利用抛物线的定义可得xP-(-1)= ,解得
,解得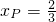 ,
,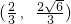 ,所以
,所以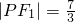 ,
,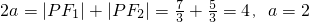 .
. ;
; 联立,得(3+4k2)x2+8kmx+4m2-12=0,
联立,得(3+4k2)x2+8kmx+4m2-12=0,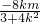 ,
,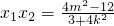 ,
,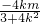 ,y0=kx0+m=
,y0=kx0+m=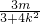 ,
,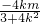 ,
,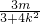 )代入曲线C的方程为y2=4x(x>0),
)代入曲线C的方程为y2=4x(x>0), ,
,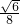 <k<
<k<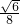 .
.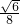 <k<
<k<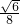 .
. ,由题意得c,由
,由题意得c,由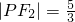 及抛物线定义可得P点横坐标,代入抛物线方程得纵坐标,由椭圆定义可得a,由b2=a2-c2可得b;.
及抛物线定义可得P点横坐标,代入抛物线方程得纵坐标,由椭圆定义可得a,由b2=a2-c2可得b;. 联立,得(3+4k2)x2+8kmx+4m2-12=0,由△>0,得4k2-m2+3>0①,由韦达定理得AB的中点(
联立,得(3+4k2)x2+8kmx+4m2-12=0,由△>0,得4k2-m2+3>0①,由韦达定理得AB的中点(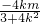 ,
,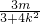 ),代入曲线C的方程为y2=4x(x>0),得9m=-16k(3+4k2),再与①联立能求出直线l的斜率k的取值范围.
),代入曲线C的方程为y2=4x(x>0),得9m=-16k(3+4k2),再与①联立能求出直线l的斜率k的取值范围.

科目:高中数学 来源:2009-2010学年广东省东莞高级中学高二(下)第一次月考数学试卷(文科)(解析版) 题型:选择题




查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com