
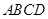 中,已知
中,已知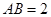 ,
,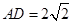 ,
, 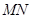 分别为
分别为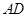 和
和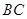 的中点,对角线
的中点,对角线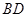 与
与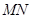 交于
交于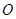 点,沿
点,沿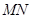 把矩形
把矩形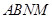 折起,使平面
折起,使平面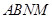 与平面
与平面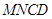 所成角为
所成角为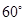 ,如图5(2).
,如图5(2).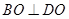 ;
;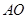 与平面
与平面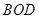 所成角的正弦值.
所成角的正弦值.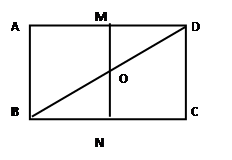

 .
. MN, BC
MN, BC MN, 折叠垂直关系不变,所以∠AMD 是平面ABMN与平面MNCD的平面角,依题意,所以∠AMD=60o,……2分
MN, 折叠垂直关系不变,所以∠AMD 是平面ABMN与平面MNCD的平面角,依题意,所以∠AMD=60o,……2分 ,所以,BD=
,所以,BD= ,由题可知BO=OD=
,由题可知BO=OD= ,由勾股定理可知三角形BOD是直角三角形,所以BO⊥DO
,由勾股定理可知三角形BOD是直角三角形,所以BO⊥DO CD, OF
CD, OF CD, 所以,CD
CD, 所以,CD 面OEF, OE
面OEF, OE CD
CD BD, OE
BD, OE 面ABCD, OE
面ABCD, OE 面BOD, 平面BOD⊥平面ABCD
面BOD, 平面BOD⊥平面ABCD
 ,BO=OD=
,BO=OD= ,
, (14分)
(14分)
 ,0,0),D(0,
,0,0),D(0, ,2),O(0,
,2),O(0, ,1
,1 (
( ,
, ,1),
,1), (0,
(0, ,
,

 0,即BO⊥DO(5分)
0,即BO⊥DO(5分) ,可得
,可得 x
x y+z=0
y+z=0 y-z=0,令
y-z=0,令 可得
可得 所以
所以
 (
( ,
, ,-1),
,-1), ,jsin
,jsin =|cos<
=|cos< >|==
>|== (14分)
(14分)

科目:高中数学 来源:不详 题型:解答题
 .
. 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,将
,将 沿AB折到
沿AB折到 的位置,使
的位置,使 ,点E在SD上,且
,点E在SD上,且 ,如下右图。
,如下右图。 平面ABCD;(2)求二面角E—AC—D的正切值.
平面ABCD;(2)求二面角E—AC—D的正切值.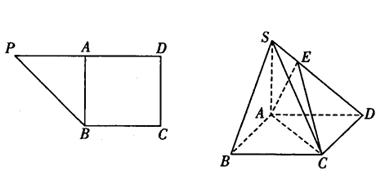
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com